Scan-Line-Verfahren für Polygone

Idee:

Bewege eine waagerechte Scan-Line schrittweise von oben nach unten über das Polygon, und berechne die Schnittpunkte der Scan-Line mit dem Polygon.

1. Sortiere alle Kanten nach ihrem größten $y$-Wert.
2. Bewege die Scan-Line vom größten $y$-Wert bis zum kleinsten $y$-Wert.
3. Für jede Position der Scan-Line
   • wird die Liste der aktiven Polygonkanten ermittelt,
   • werden die Schnittpunkte berechnet und nach 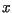$x$-Werten sortiert,
   • werden jene Scan-Line-Segmente, die im Inneren des Polygons liegen, angezeigt.

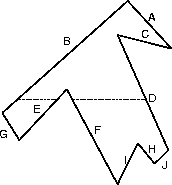
Abbildung 4.4 zeigt eine Scanline beim Durchqueren eines Polygons. Die Sortierung der Kanten nach ihrem größten $y$-Wert ergibt die Folge $A B C D E F G H I J$. Die zur Zeit aktiven Kanten sind $B E F D$. Die sortierten $x$-Werte der Schnittpunkte $x_{1}, x_{2}, \ldots, x_n$ ergeben die zu zeichnenden Segmente $(x_{1}, x_{2}), (x_{3}, x_{4}), \ldots$

Abbildung 4.4: Polygon mit Scanline

Die Sortierung der Kanten nach ihren größten $y$-Werten ermöglicht den einfachen Aufbau und die effiziente Aktualisierung einer Liste von aktiven Kanten. Eine Kante wird in diese Liste aufgenommen, wenn der Endpunkt mit dem größeren $y$-Wert von der Scan-Line überstrichen wird, und wird wieder entfernt, wenn die Scan-Line den anderen Endpunkt überstreicht.

Horizontale Kanten werden nicht in die Kantenliste aufgenommen. Für sie wird eine Linie gezeichnet.

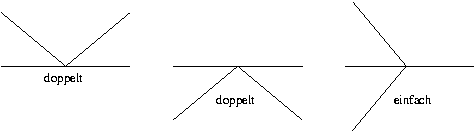
Trifft die Scan-Line auf einen Polygoneckpunkt, dessen Kanten beide oberhalb oder beide unterhalb liegen, so zählt der Schnittpunkt doppelt. Trifft die Scan-Line auf einen Polygoneckpunkt, dessen Kanten oberhalb und unterhalb liegen, so zählt der Schnittpunkt nur einfach (siehe Abbildung 4.5 ).

Dadurch wird sichergestellt, daß die Paare $(x_{1}, x_{2}), (x_{3}, x_{4}), \ldots$ der sortierten $x$-Werte der Schnittpunkte die zu zeichnenden Segmente im Inneren korrekt darstellen.

Abbildung 4.5: Fallunterscheidungen beim Berechnen der Schnittpunkte

Kohärenz-Eigenschaft

Abbildung 4.6 zeigt, wie die Schnittpunkte für Scan-Line $y_{i + 1}$ sich mit Hilfe der Schnittpunkte von Scan-Line $y_i$ bestimmen lassen.

Abbildung 4.6: Fortschreiben der errechneten Schnittpunkte

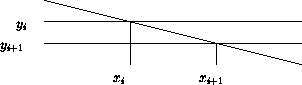
Es gilt: Die Steigung der Geraden lautet $s=(y_{i}-y_{i+1}) / (x_{i}- x_{i+1})$.
Wegen $y_{i}-y_{i+1}=1$ ergibt sich $x_{i + 1} = x_{i} - 1/s$.

Abbildung 4.7: Vom Scanline-Algorithmus gefülltes Polygon