| X | XXXXXXXX | XXXXXXXXXXXXXXXXXXXXXXX |
| Vorzeichen s | Exponent e | Mantisse f |
![]() =
= 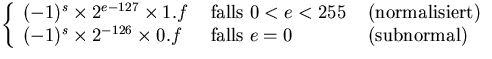
Bei einer normalisierten Darstellung liegt der Wert der Mantisse 1.f im Intervall [1,2[ .
Hierbei haben Dualzahlen nach dem Komma
0.d- 1d- 2d- 3...d- k![]()
![]() di · 2i
di · 2i
Algorithmus dezimal ![]() dual:
dual:
Sei Dezimalzahl x gegeben.
Bestimme größte 2 -er Potenz 2d mit 2d ![]() x .
Setze
f = (x - 2d)/2d.
Offenbar gilt
x .
Setze
f = (x - 2d)/2d.
Offenbar gilt
x = (1 + f ) · 2d![]() 0
0 ![]() f < 1.
f < 1.
Bestimme die Dualzahl-Bits von f durch
for (i = 0; i < 23; i++) {
f = f * 2.0;
if (f >= 1.0) {IO.print('1'); f = f - 1.0;}
else IO.print('0');
}
| s | = | 0 | |
| f | = |
(13.5 - 23)/23 = 0.6875 = | |
| e | = | 3 + 127 = 130 |
| 0 | 10000010 | 10110000000000000000000 |
| Vorzeichen | Exponent | Mantisse |
Bei einer subnormalisierten Darstellung liegt der Wert der Mantisse 0.f im Intervall [0,1[ .
Exponent e = 0 und Mantisse f = 0 repräsentieren
die vorzeichenbehaftete Null.
Exponent e = 255 und Mantisse f = 0 repräsentieren
das vorzeichenbehaftete Unendlich(
+ ![]() , -
, - ![]() ).
Exponent e = 255 und Mantisse f
).
Exponent e = 255 und Mantisse f ![]() 0 repräsentieren
die undefinierte Zahl NaN (not a number).
0 repräsentieren
die undefinierte Zahl NaN (not a number).
Beispiel: 2- 130 = 1/16 · 2- 126
Daraus folgt
| s | = | 0 | |
| f | = | 0.0625 = 1/16 | |
| e | = | 0 |
Codierung
| 0 | 00000000 | 00010000000000000000000 |
| Vorzeichen | Exponent | Mantisse |
Die größte darstellbare positive Zahl liegt knapp unter
2 · 2254 - 127 = 2128 ![]() 1038
1038
| 0 | 11111110 | 11111111111111111111111 |
| Vorzeichen | Exponent | Mantisse |
Die kleinste darstellbare positive Zahl lautet
2- 23 · 2- 126 = 2- 149 ![]() 10- 45
10- 45
| 0 | 00000000 | 00000000000000000000001 |
| Vorzeichen | Exponent | Mantisse |
Bei der Codierung für 64 Bits (double) benötigt das Vorzeichen 1 Bit, der Exponent 11 Bits, die Mantisse 52 Bits.
| X | XXXXXXXXXXX | XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX |
| Vorzeichen s | Exponent e | Mantisse f |
![]() =
= 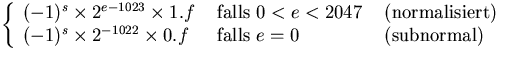
Damit liegt die größte darstellbare positive Zahl knapp unter
2 · 22046 - 1023 ![]() 10308
10308
Die kleinste darstellbare positive Zahl lautet
2- 52 · 2- 1022 = 2- 1074 ![]() 10- 324
10- 324
| + | : | Gleitkomma × Gleitkomma | |
Gleitkomma | Addition |
| - | : | Gleitkomma × Gleitkomma | |
Gleitkomma | Subtraktion |
| * | : | Gleitkomma × Gleitkomma | |
Gleitkomma | Multiplikation |
| / | : | Gleitkomma × Gleitkomma | |
Gleitkomma | Division |
| % | : | Gleitkomma × Gleitkomma | |
Gleitkomma | Modulo |
| ++ | : | Gleitkomma | |
Gleitkomma | Inkrement um 1.0 |
| -- | : | Gleitkomma | |
Gleitkomma | Dekrement um 1.0 |
Multiplikation: (Exponenten addieren, Mantissen multiplizieren)
| Beispiel: | 12 | * | 20 | = | ||
| 1.5 · 23 | * | 1.25 · 24 | = | |||
| 1.5 · 1.25 | * | 23 · 24 | = | |||
| 1.875 | * | 27 | = | 240 |
Addition: (Exponenten angleichen, Mantissen addieren)
| Beispiel: | 12 | + | 20 | = | ||
| 1.5 · 23 | + | 1.25 · 24 | = | |||
| 0.75 · 24 | + | 1.25 · 24 | = | |||
| (0.75 + 1.25) | * | 24 | = | |||
| 1 | * | 25 | = | 32 |
Problem beim Angleichen der Exponenten:
| Beispiel: | 1024 | + |
|
= | ||
| 1 · 210 | + | 1 · 2- 20 | = | |||
| 1 · 210 | + | 2- 30 · 210 | = | |||
| 1 · 210 | + | 0 · 210 | = | 1024 |
Bei 23 Bits für die Mantisse ist 2- 30 nicht mehr darstellbar.
Gleitkommaoperationen stoßen in Java keine Ausnahmebehandlung an.
D.h., Division durch Null führt nicht zum Abbruch, sondern ergibt den
Wert + ![]() bzw. -
bzw. - ![]() ;
Null dividiert durch Null ergibt NaN (not a number).
;
Null dividiert durch Null ergibt NaN (not a number).
| Beispiele: | .2 | ||||
| 2 | |||||
| 2. | |||||
| 2.0 | |||||
| 2.538 | |||||
| 2.538f | |||||
| 2.5E2 | = | 2.5*102 | = | 250 | |
| 2.5E-2 | = | 2.5*10- 2 | = | 0.025 |
Source:
Gleitkomma.java
JavaDoc:
Gleitkomma.html
Applet:
