O-Notation

Seien f, g : N N

f ist höchstens von der Größenordnung g

in Zeichen: f O(g)

falls n₀, c   N existieren mit

 n   n₀ :  f (n)   c  ^.  g(n) .

Statt f O(g) sagt man auch f = O(g)

Wegen des konstanten Faktors c ist die exakte Festlegung eines Schrittes nicht erforderlich.

Beispiel:

Sei f (n) = 31n + 12n².

Dann ist f O(n²)

Natürlich gilt auch: f O(n⁷) Die wesentlichen Klassen

log n	n	n . log n	n2	n3	n4	...	2n	3n	n!
binäre	lineare	schlaues	dummes	Gleichungs-			alle		alle
Suche	Suche	Sortieren	Sortieren	system			Teil-		Permu-
				lösen			mengen		tationen

Annahme: 1 Schritt dauert 1 s = 0.000001 s

n =	10	20	30	40	50	60
n	10 s	20 s	30 s	40 s	50 s	60 s
n2	100 s	400 s	900 s	1.6 ms	2.5 ms	3.6 ms
n3	1 ms	8 ms	27 ms	64 ms	125 ms	216 ms
2n	1 ms	1 s	18 min	13 Tage	36 J	366 Jh
3n	59 ms	58 min	6.5 J	3855 Jh	108 Jh	1013 Jh
n!	3.62 s	771 Jh	1016 Jh	1032 Jh	1049 Jh	1066 Jh

Für einen Algorithmus mit Laufzeit O(2ⁿ) gilt daher:

Wächst n um 1, so wächst 2ⁿ um den Faktor 2.
Wächst n um 10, so wächst 2ⁿ um den Faktor 2¹⁰ = 1024.
Ein 1000-mal schnellerer Computer kann eine um 10 Daten größere Eingabe in derselben Zeit bearbeiten.

Analoge Aussagen sind möglich bzgl. Speicherplatz.
Wir zählen nicht die Anzahl der Bytes, sondern betrachten das Wachstum des Platzbedarfs in Speicherplätzen in Abhängigkeit von der Größe der Eingabe.

Aussagen über Laufzeit und Platzbedarf beziehen sich auf

best case	günstigster Fall
worst case	ungünstigster Fall
average case	im Mittel

Analyse von for-Schleifen

Beispiel:

Minimumsuche in einem Array der Länge n

min = a[0];
for (i = 1; i < n; i++){
       if(a[i] < min) min = a[i];
}

Laufzeit O(n) für	best case
	worst case
	average case.

Beispiele:

for (i = 0; i < k; i++) {             for (i = 0, i < k; i++) {
   for (j = 0; j < k; j++) {             for (j = 0; j < k; j++) {
      brett[i][j] = 0;                      if (a[i] == a[j]) treffer = true;
   }                                     }
}                                     }

k2 Schritte für k2 Daten		k2 Schritte für k Daten
O(n) -Algorithmus		O(n2) -Algorithmus

Analyse von while-Schleifen

Beispiel:

Lineare Suche im Array

i = 0;
while (i < n) && (a[i] != x) {
   i++;
}

Laufzeit:	best case	1 Schritt		O(1)
	worst case	n Schritte		O(n)
	average case	Schritte		O(n)

Annahme für den average case:
Es liegt Permutation der Zahlen von 1 bis n vor.
Dann ist die mittlere Anzahl

Beispiel:

Suche 0 in einem Array, bestehend aus Nullen und Einsen.

Laufzeit:	best case	1 Schritt		O(1)
	worst case	n Schritte		O(n)
	average case	i . 2		O(1)

Obacht:

Alle Laufzeitangaben beziehen sich jeweils auf einen konkreten Algorithmus A (für ein Problem P) = obere Schranke für Problem P.

Eine Aussage darüber, wie viele Schritte jeder Algorithmus für ein Problem P mindestens durchlaufen muss, nennt man untere Schranke für Problem P.

Beispiel: naives Pattern-Matching

char[] s = new char[N];                            // Zeichenkette
char[] p = new char[M];                            // Pattern

Frage: Taucht Pattern p in Zeichenkette s auf?

for (i = 0; i <= N - M; i++) {                     // Index in Zeichenkette
   for (j = 0; (j < M) && (p[j] == s[i+j]); j++);  // Index im Pattern
   if (j == M) break;                              // Erfolg
}

Laufzeit best case:	O(1)
Laufzeit worst case:	(N - M + 1) . M Vergleiche für	s	=	AAA...AB
		p	=	A...AB

Sei n die Summe der Buchstaben in Pattern p und String s. Sei M = x ^. n und N = (1 - x) ^. n für 0 < x < 1.

Gesucht wird x, welches ((1 - x) ^. n - x ^. n + 1) ^. x ^. n = (n² + n) ^. x - 2n^{2 .} x² maximiert.

Bilde 1. Ableitung nach x und setze auf 0: 0 = n² + n - 4n^{2 .} x

1. [ ] Maximum liegt bei    

Also können (n - n + 1) ^. n = n² + n Vergleiche entstehen.

1. [ ] Die Laufzeit im worst case beträgt O(n²).

Analyse eines rekursiven Programms

Beispiel:

Die Laufzeit von fib(n) beträgt:

f (n) =

Offenbar gilt: f O() für ein < 2 (denn f (n) = f (n - 1) + f (n - 1) würde zu O(2ⁿ) führen).

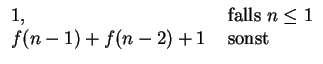
Gesucht ist also ein , so dass für große n gilt:

= + + 1

Teile durch :

= + 1 + . Für n und > 1 geht 0.

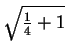= + 1 = + = 1.61803 (gemäß Formel - )

Das rekursive Fibonacci-Programm hat die Laufzeit O(1.62ⁿ), wobei n der Wert des Inputs ist, nicht seine Länge!

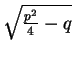für n = 20 ist	1.62n	15.000
	2n	1.000.000.