


Previous: Codierung
Up: Gleitkommazahlen (float, double)
Next: Konstantenbezeichner
| + |
: |
Gleitkomma 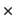 Gleitkomma Gleitkomma |
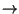 |
Gleitkomma |
Addition |
| - |
: |
Gleitkomma 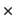 Gleitkomma Gleitkomma |
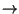 |
Gleitkomma |
Subtraktion |
| * |
: |
Gleitkomma  Gleitkomma Gleitkomma |
 |
Gleitkomma |
Multiplikation |
| / |
: |
Gleitkomma  Gleitkomma Gleitkomma |
 |
Gleitkomma |
Division |
| % |
: |
Gleitkomma  Gleitkomma Gleitkomma |
 |
Gleitkomma |
Modulo |
| ++ |
: |
Gleitkomma |
 |
Gleitkomma |
Inkrement um 1.0 |
| -- |
: |
Gleitkomma |
 |
Gleitkomma |
Dekrement um 1.0 |
Multiplikation: (Exponenten addieren, Mantissen multiplizieren)
Addition: (Exponenten angleichen, Mantissen addieren)
Problem beim Angleichen der Exponenten:
Bei 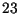 Bits für die Mantisse ist
Bits für die Mantisse ist 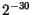 nicht mehr darstellbar.
nicht mehr darstellbar.
Gleitkommaoperationen stoßen in Java keine Ausnahmebehandlung an.
D.h., Division durch Null führt nicht zum Abbruch, sondern ergibt den
Wert 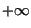 bzw.
bzw. 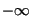 ;
Null dividiert durch Null ergibt NaN (not a number).
;
Null dividiert durch Null ergibt NaN (not a number).



Previous: Codierung
Up: Gleitkommazahlen (float, double)
Next: Konstantenbezeichner