Analyse von while-Schleifen

Beispiel:

Lineare Suche im Array

i = 0;
while (i < n) && (a[i] != x) {
   i++;
}

Laufzeit:	best case	$1$ Schritt	$\Rightarrow$	$O(1)$
	worst case	$n$ Schritte	$\Rightarrow$	$O(n)$
	average case	$\frac{n}{2}$ Schritte	$\Rightarrow$	$O(n)$

Annahme für den average case:
Es liegt Permutation der Zahlen von $1$ bis $n$ vor.
Dann ist die mittlere Anzahl

$$\begin{eqnarray*} = \frac{1}{n}\sum_{i=1}^{n} i& {\approx}& \frac{n}{2}\ \end{eqnarray*}$$

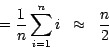
Beispiel:

Suche $0$ in einem Array, bestehend aus Nullen und Einsen.

Laufzeit:	best case	$1$ Schritt	$\Rightarrow$	$O(1)$
	worst case	$n$ Schritte	$\Rightarrow$	$O(n)$
	average case	$\sum\limits_{i=1}^{n} i \cdot \frac{1}{2^i} \leq 2$	$\Rightarrow$	$O(1)$

Obacht:

Alle Laufzeitangaben beziehen sich jeweils auf einen konkreten Algorithmus $A$ (für ein Problem $P$) = obere Schranke für Problem $P$.

Eine Aussage darüber, wie viele Schritte jeder Algorithmus für ein Problem $P$ mindestens durchlaufen muss, nennt man untere Schranke für Problem $P$.

Beispiel: naives Pattern-Matching

char[] s = new char[N];                            // Zeichenkette
char[] p = new char[M];                            // Pattern

Frage: Taucht Pattern $p$ in Zeichenkette $s$ auf?

for (i = 0; i < N - M + 1; i++) {                  // Index in Zeichenkette
   for (j = 0; (j < M) && (p[j] == s[i+j]); j++);  // Index im Pattern
   if (j == M) break;                              // Erfolg
}

Laufzeit best case:	$O(1)$
Laufzeit worst case:	$(N-M+1)\cdot M$ Vergleiche für	$s$	=	$AAA\ldots AB$
		$p$	=	$A\ldots AB$

Sei $n$ die Summe der Buchstaben in Pattern $p$ und String $s$. Sei $M=x \cdot n$ und $N=(1-x)\cdot n$ für $0<x<1$.

Gesucht wird $x$, welches $((1-x)\cdot n-x \cdot n+1)\cdot x\cdot n=(n^{2} +n)\cdot x-2 n^{2} \cdot x^2$ maximiert.

Bilde 1. Ableitung nach $x$ und setze auf 0: $0= n^2+n-4 n^{2} \cdot x$

1. [$\Rightarrow$] Maximum liegt bei $\frac{n^{2} +\ n}{4 n^2}\ \approx\ \frac{1}{4}$

Also können $(\frac{3}{4} n- \frac{1}{4} n+1 )\cdot \frac{1}{4} n= \frac{1}{8}n^{2} + \frac{1}{4} n$ Vergleiche entstehen.

1. [$\Rightarrow$] Die Laufzeit im worst case beträgt $O( n^2 )$.