


Previous: Analyse von while-Schleifen
Up: O-Notation
Next: Korrektheit und Terminierung
Beispiel:
Die Laufzeit von 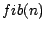 beträgt:
beträgt:
Offenbar gilt:
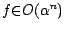 für ein
für ein 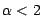 (denn
(denn
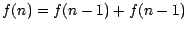 würde zu
würde zu 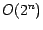 führen).
führen).
Gesucht ist also ein 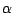 , so dass für große
, so dass für große 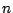 gilt:
gilt:
Teile durch 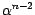 :
:
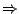
-
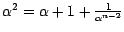 .
Für
.
Für
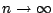 und
und 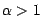 geht
geht
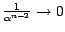 .
.
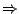
-
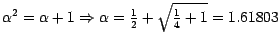 (gemäß Formel
(gemäß Formel
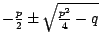 )
)
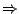
- Das rekursive Fibonacci-Programm hat die Laufzeit
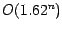 , wobei
, wobei 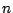 der Wert des Inputs ist, nicht seine
Länge!
der Wert des Inputs ist, nicht seine
Länge!



Previous: Analyse von while-Schleifen
Up: O-Notation
Next: Korrektheit und Terminierung
![]() beträgt:
beträgt:
![]() , so dass für große
, so dass für große ![]() gilt:
gilt:
![]() :
: