Zunächst wird für jede Farbe die Häufigkeit ihres Auftretens ermittelt. Hierdurch erhält man ein Histogramm.
Sei d (a,b) der Abstand zweier Farbtupel a,b ,
z.B. 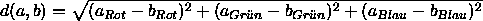 .
.
Optimaler Algorithmus
Gegeben sei eine Menge F von beobachteten Farben.
Gesucht ist eine Menge M von k Repräsentanten, so daß der Ausdruck
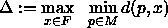
minimiert wird, d.h., ![]() ist der maximale Abstand, den eine Farbe zu ihrem
nächsten Repräsentanten hat.
ist der maximale Abstand, den eine Farbe zu ihrem
nächsten Repräsentanten hat.
Da die exakte Bestimmung von M eine exponentielle Laufzeit
verursacht, begnügt man sich mit einer Näherungslösung.
Popularity-Algorithmus (1978)
Wähle die k häufigsten Farben.
Nachteil: Selten vorkommende Farben werden schlecht
repräsentiert.
Diversity-Algorithmus ( xv , John Bradley, 1989)
Initialisiere M mit der häufigsten Farbe.
for i := 2 to k do erweitere M um die Farbe des Histogramms, die zu allen Farben aus M den groessten Abstand hat end
Median-Cut (Heckbert, MIT 1980)
Initialisiere RGB-Wuerfel mit Haeufigkeiten der beobachteten Farbtupel Initialisiere Wurzel des Schnittbaums mit Gesamtzahl der Pixel While noch_nicht_genuegend_Blaetter do Waehle Blatt mit der groessten Pixelzahl Bestimme umschliessende Box Bestimme Achse mit groesstem Wertebereich Durchlaufe Box laengs dieser Achse Teile am Median in zwei Haelften Trage Haelften als Soehne ein end Fuer jedes Blatt waehle den Mittelwert aller in ihm liegenden Farben.
Der Median-Cut-Algorithmus von Heckbert wird verwandt im Programm ppmquant, das Teil des PBM-Pakets ist.