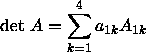Analog zum zweidimensionalen Fall werden die dreidimensionalen Transformationen durch Verknüpfung homogener Koordinaten mit 4 × 4 -Transformationsmatrizen dargestellt.
Sei
A = (aik) ,
1 ![]() i,k
i,k ![]() 4 , eine 4 × 4 -Matrix:
4 , eine 4 × 4 -Matrix:
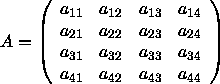
Ist D = det A = |aik| die Determinante von A , so bezeichnet man als Unterdeterminante des Elementes aik diejenige 3-reihige Determinante, die aus D durch Streichen der i -ten Zeile und der k -ten Spalte hervorgeht. Unter der Adjunkten Aik des Elementes aik versteht man die mit dem Faktor (- 1)i + k versehene Unterdeterminante von aik .
Beispiel:
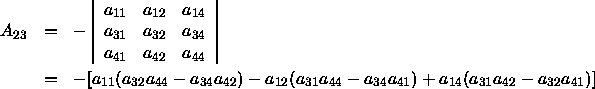
Für die inverse Matrix A - 1 gilt:
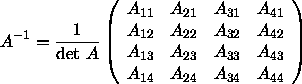
Für die Entwicklung
der Determinante von A nach der ersten Zeile können die Adjunkten benutzt werden.
Es gilt: