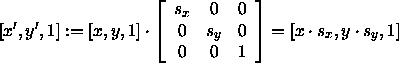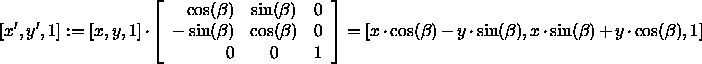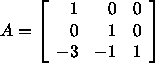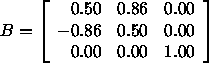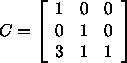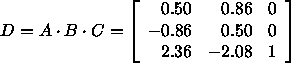Häufig werden mehrere Transformationen hintereinander auf ein Objekt
angewendet.
Es entstehen Rundungsfehler, wenn nach jeder Einzel-Transformation
die ganzzahligen Koordinaten bestimmt werden.
Deshalb sollten mehrere Transformationen zu einer zusammengesetzt werden.
Def.: Ein Punkt P = (x,y) hat die homogenen Koordinaten
[xh,yh,w] mit w 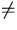 0 und
0 und
- Beispiel:
- Das homogene Koordinatentripel [6,8,2]
gehört zum Punkt P = (3,4) , [3,4,1] auch.
Ein Richtungsvektor R = (x,y) hat die homogenen Koordinaten
[x,y,0] .
- Beispiel:
- Das homogene Koordinatentripel [3,4,0] gehört zum
Richtungsvektor (3,4) .
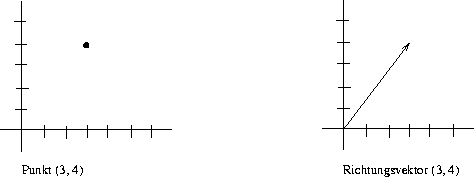
Die Transformationen Translation, Skalierung und Rotation werden nun
als 3 × 3 -Matrizen realisiert.
Zusammengesetzte Transformationen ergeben sich durch Matrix-Multiplikation.
Translation
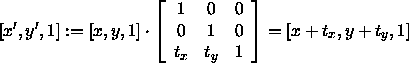
Skalierung
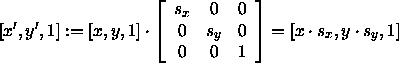
Rotation
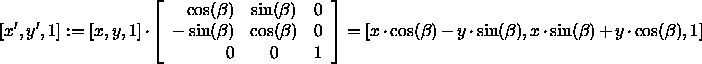
Für die Auswertung einer zusammengesetzten Transformation
- gilt das Assoziativgesetz, d.h.
A · B · C = (A · B) · C = A · (B · C) ,
- gilt im allgemeinen nicht das Kommutativgesetz, d.h.
A · B
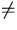 B · A .
B · A .
- Beispiel:
- Translation um (- 3, - 1) mit anschließender Rotation um
90 o ist verschieden von Rotation um 90 o mit
anschließender Translation um (- 3, - 1) .
- Beispiel:
- Rotation bzgl. (3,1) um 60 o
Matrix für Translation um (- 3, - 1) lautet
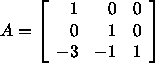
Matrix für Rotation um 60 o lautet
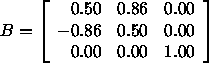
Matrix für Translation um (3,1) lautet
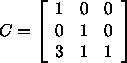
Matrix für gesamte Transformation lautet
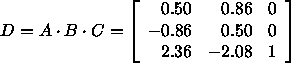




![]() 0 und
0 und