Device Mapping

Die abschließende Projektion der Szene in Schritt 4.) aus dem NPC auf den Bildschirm wird als Device Mapping bezeichnet. Der Einheitswürfel enthält dank der vorangegangenen Transformationen die gesamte darzustellende Szeneninformation. Die Abbildung muß lediglich die $x$- und $y$-Koordinaten aus dem NPC so in die Bildschirmkoordinaten DC (Device Coordinate System) transformieren, daß eine anschließende Rundung die ganzzahligen Koordinaten der Pixel ergibt.

DC ist auf den meisten Bildschirmen ein linkshändiges Koordinatensystem. (Die $y$-Achse zeigt nach unten, oben links ist der Ursprung $(0,0)$.) Die Anzahl der Pixel im Ausgabefenster ist flexibel und betrage horizontal $xsize$ und vertikal $ysize$. In $x$-Richtung muß dann das Intervall $[0,1]$ auf die diskreten Werte $\{0, ..., xsize-1 \}$ und in $y$-Richtung $[0,1]$ umgekehrt auf $\{ ysize-1, ... , 0 \}$ abgebildet werden. Die $z$-Koordinaten dienen später zur Bestimmung und Unterdrückung verdeckter Flächen, die sich durch die Staffelung der Objekte in der Tiefe des Bildraumes ergeben.

Abbildung 13.9: Device Mapping

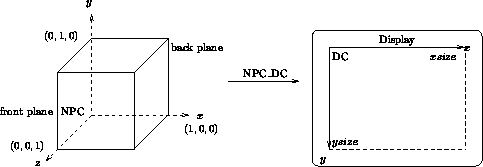
Die Transformationsmatrix entspricht einer Skalierung um den Vektor $(xsize, -ysize, 1)$ konkateniert mit einer Translation des Ursprungs in die linke untere Ecke des Bildschirms $(0, ysize, 0)$.

$$T_{\hbox{\scriptsize NPC\_DC}} = \left[ \begin{array}{cccc} ... ...\ 0&-ysize&0&ysize\\ 0&0&1&0\\ 0& 0&0&1 \end{array} \right]$$

Für die Projektion werden einfach die $x$- und $y$-Werte übernommen; die $z$-Werte sind erforderlich zur Regelung der Sichtbarkeit.