Back-Face Removal/Culling

Ein Körper besteht aus Flächen, die dem Betrachter zugewandt sind (sogenannte Vorderflächen oder Front Faces) und solchen, die vom Betrachter abgewandt sind (sogenannte Rückflächen oder Back Faces). Die Rückflächen sind nicht sichtbar, da sie stets von Vorderflächen verdeckt sind. Die Unterdrückung der Rückflächen (Back-Face Removal oder Back-Face Culling) ist daher ein erster Schritt in Richtung einer natürlichen Darstellung des Kantenmodells. Für einen konvexen Körper bestimmt das Back-Face Culling exakt den sichtbaren Teil. Ist er dagegen nicht konvex, so werden zwar mehr Kanten angezeigt, als wirklich sichtbar sind, die Darstellung ist jedoch schon sehr realistisch. Ein weiterer Aspekt ist, daß bei einer komplexen Szene circa die Hälfte aller Flächen Rückflächen sind. Durch ihren Ausschluß halbieren sich in etwa die weiteren Berechnungen für Lighting und Shading.

Das Programm benutzt eine sehr effiziente Methode unter Verwendung der Normalenvektoren, um Vorder- und Rückflächen zu unterscheiden. Für die Flächen eines Objekts sind die Normalen so definiert, daß sie nach außen zeigen. Liegt der Betrachterstandpunkt auf der Außenseite einer Fläche, so handelt es sich um eine Vorder-, sonst um eine Rückfläche.

Wenn $\vec{n}$ der Normalenvektor der Fläche und $\vec{a}$ ein Eckpunkt ist, dann kann hieraus die Gleichung der Ebene, in der die Fläche liegt, in der Hesseschen Normalform bestimmt werden:

$$\vec{p} \cdot \vec{n} - \vec{a} \cdot \vec{n}= e.$$

Beim Einsetzen verschiedener Punkte $\vec{p}$ ergeben sich unterschiedliche Werte für $e$. Gilt $e = 0$, so liegt $\vec{p}$ in der Ebene, bei $e > 0$ befindet sich $\vec{p}$ außen, d.h., die Fläche ist von $\vec{p}$ aus sichtbar, und bei $e < 0$ liegt $\vec{p}$ innen, d.h., die Fläche ist von $\vec{p}$ aus unsichtbar.

Abbildung 16.1: Back-Face Removal mit Hessescher Normalform

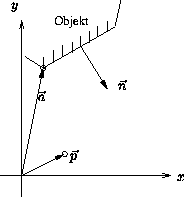
Um die Rückflächen zu erkennen, ist für alle Flächen die obige Ebenengleichung zu berechnen, in die der Betrachterstandpunkt eingesetzt wird. Ergibt sich $e \geq 0$, so handelt es sich um eine Vorderfläche, sonst um eine Rückfläche. Dabei ist zu beachten, daß ggf. für jeden Eckpunkt eine eigene Normale definiert ist. Dies ist zum Approximieren von gekrümmten Flächen notwendig. Bei einer Rückfläche sind definitionsgemäß alle Normalenvektoren abgewandt. Flächen, bei denen einige Normalen zum Betrachter und andere von ihm weg zeigen, werden teilweise dargestellt. Es ist Aufgabe des später vorzustellenden Shaders, die sichtbaren Pixel zu bestimmen. Bei der Liniendarstellung wird eine Kante gezeichnet, wenn mindestens ein Eckpunkt sichtbar ist.

Eine algorithmische Vereinfachung des Tests auf Sichtbarkeit ergibt sich durch die Transformation der Ebenengleichung ins NPC. Hierbei wird ausgenutzt, daß der Betrachterstandpunkt im NPC per Definition die homogenen Koordinaten $(0, 0, 1, 0)$ besitzt. (Er liegt im Unendlichen auf der positiven $z$-Achse.) Daraus folgt, daß das Skalarprodukt zwischen Ebene und Betrachterstandpunkt im NPC identisch mit der $z$-Komponente des homogenen Normalenvektors der Fläche ist.

Zur Klassifizierung des Flächentyps wird daher im Programm zunächst nur die $z$-Komponente der homogenen Normalenvektoren ins NPC transformiert. Durch diese sehr effiziente Methode, Rückflächen zu eliminieren, halbiert sich in etwa die Berechnung zur Darstellung eines Objekts.