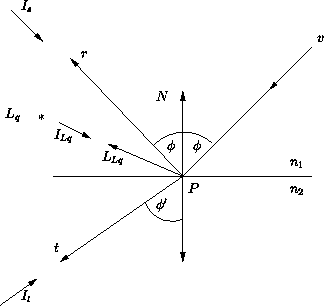
Der rekursive Ray-Tracing-Algorithmus startet zusätzlich zu den
Schattenstrahlen weitere Spiegelungs- und Brechungsstrahlen
im Schnittpunkt (siehe Abbildung
21.4
).
Diese Spiegelungs-, Reflexions- und
Brechungsstrahlen heißen Sekundärstrahlen, um sie von
den Primärstrahlen zu unterscheiden, die vom Auge ausgehen.
Gibt es bei dem Objekt spiegelnde Reflexion, dann wird ein
Spiegelungsstrahl um die Flächennormale in Richtung ![]() gespiegelt.
Ist das Objekt transparent, und es gibt keine totale innere Reflexion,
startet man einen Brechungsstrahl entlang
gespiegelt.
Ist das Objekt transparent, und es gibt keine totale innere Reflexion,
startet man einen Brechungsstrahl entlang ![]() in das Objekt.
Der Winkel wird nach dem Gesetz von Snellius bestimmt.
in das Objekt.
Der Winkel wird nach dem Gesetz von Snellius bestimmt.
Jeder dieser Reflexions- und Brechungsstrahlen kann wiederum neue Spiegelungs-, Reflexions- und Brechungsstrahlen starten.
Typische Bestandteile eines Ray-Tracing-Programms sind die Prozeduren shade und intersect, die sich gegenseitig aufrufen. shade berechnet die Farbe eines Punktes auf der Oberfläche. Hierzu werden die Beiträge der reflektierten und gebrochenen Strahlen benötigt. Diese Beiträge erfordern die Bestimmung der nächstgelegenen Schnittpunkte, welche die Prozedur intersect liefert. Der Abbruch der Strahlverfolgung erfolgt bei Erreichen einer vorgegebenen Rekursionstiefe oder wenn ein Strahl kein Objekt trifft.
Seien ![]() die normierten Vektoren für Sehstrahl und Normale.
Sei
die normierten Vektoren für Sehstrahl und Normale.
Sei ![]() das Verhältnis der beiden Brechungsindizes.
Dann sind die Vektoren
das Verhältnis der beiden Brechungsindizes.
Dann sind die Vektoren ![]() und
und ![]() , die im Schnittpunkt
, die im Schnittpunkt ![]() zur
Weiterverfolgung des reflektierten und gebrochenen Strahls benötigt
werden, definiert durch
zur
Weiterverfolgung des reflektierten und gebrochenen Strahls benötigt
werden, definiert durch
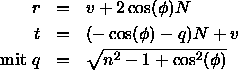
Ist ![]() ein imaginärer Ausdruck, liegt Totalreflexion vor,
und der Transmissionsanteil wird gleich Null gesetzt.
ein imaginärer Ausdruck, liegt Totalreflexion vor,
und der Transmissionsanteil wird gleich Null gesetzt.
In die Berechnung der Farbe im Punkt ![]() geht
die gewichtete Summe der in den einzelnen
Rekursionsschritten berechneten Farbintensitäten ein.
Unter Berücksichtigung des
Phong-Modells
ergibt sich
geht
die gewichtete Summe der in den einzelnen
Rekursionsschritten berechneten Farbintensitäten ein.
Unter Berücksichtigung des
Phong-Modells
ergibt sich
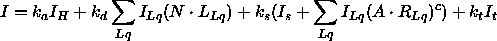
mit
| ambienter Reflexionskoeffizient | |
| Hintergrundbeleuchtung | |
| diffuser Reflexionskoeffizient | |
| Intensität der Lichtquelle | |
| Normale auf Ebene | |
| Vektor zur Lichtquelle | |
| spiegelnder Reflexionskoeffizient | |
| globale Reflexionssintensität | |
| Vektor zum Augenpunkt | |
| Reflexionsvektor für Lichtquelle |
|
| spekularer Exponent | |
| Transmissionskoeffizient (materialabhängig) | |
| Transmissionsintensität |
Pseudocode für einfaches rekursives Ray Tracing
Wähle Projektionszentrum und Window in der view plane;
for(jede Rasterzeile des Bildes){
for(jedes Pixel der Rasterzeile){
Ermittle Strahl vom Projektionszentrum durch das Pixel;
pixel = RT_intersect(ray, 1);
}
}
/* Schneide den Strahl mit Objekten, und berechne die Schattierung am nächsten */
/* Schnittpunkt. Der Parameter depth ist die aktuelle Tiefe im Strahlenbaum. */
RT_color RT_intersect(RT_ray ray, int depth)
{
Ermittle den nächstliegenden Schnittpunkt mit einem Objekt;
if(Objekt getroffen){
Berechne die Normale im Schnittpunkt;
return RT_shade(nächstliegendes getroffenes Objekt, Strahl, Schnittpunkt,
Normale, depth);
}
else
return HINTERGRUND_FARBE;
}
/* Berechne Schattierung für einen Punkt durch Verfolgen der Schatten-, */
/* Reflexions- und Brechungsstrahlen */
RT_color RT_shade(
RT_object object,
/* Geschnittenes Objekt */
RT_ray ray,
/* Einfallender Strahl */
RT_point point,
/* Schnittpunkt, der schattiert werden soll */
RT_normal normal,
/* Normale in dem Punkt */
int depth)
/* Tiefe im Strahlenbaum */
{
RT_color color;
/* Farbe des Strahls */
RT_ray rRay, tRay, sRay;
/* Reflexions-, Brechungs- und Schattenstrahlen */
RT_color rColor, tColor;
/* Farbe des reflektierten und gebrochenen Strahls */
color = Term für das ambiente Licht;
for(jede Lichtquelle){
sRay = Strahl von der Lichtquelle zum Punkt;
if(Skalarprodukt der Normalen mit der Richtung zum Licht ist positiv){
Berechne, wieviel Licht von opaken und transparenten Flächen blockiert wird;
Skaliere damit die Terme für diffuse und spiegelnde Reflexion, bevor sie
zur Farbe addiert werden;
}
}
if(depth < maxDepth){
/* Bei zu großer Tiefe beenden */
if(Objekt reflektiert){
rRay = Strahl vom Punkt in Reflexionsrichtung;
rColor = RT_intersect(rRay, depth + 1);
Skaliere rColor mit dem Spiegelungskoeffizienten,
und addiere den Wert zur Farbe;
}
if(Objekt ist transparent){
tRay = Strahl vom Punkt in Brechungsrichtung;
if(es gibt keine totale interne Reflexion){
tColor = RT_intersect(tRay, depth + 1);
Skaliere tColor mit dem Transmissionskoeffizienten,
und addiere den Wert zur Farbe;
}
}
}
return color;
/* Liefere die Farbe des Strahls zurück */
}
Ray Tracing ist besonders anfällig für Probleme, die durch die
begrenzte Rechengenauigkeit entstehen.
Dies zeigt sich vor allem bei der Berechnung der Schnittpunkte
sekundärer Strahlen mit den Objekten.
Wenn man die ![]() -,
-, ![]() - und
- und ![]() -Koordinaten eines Objekts mit
einem Augstrahl berechnet hat, dienen sie zur Definition des
Startpunkts eines Sekundärstrahls.
Für diesen muß dann der Parameter
-Koordinaten eines Objekts mit
einem Augstrahl berechnet hat, dienen sie zur Definition des
Startpunkts eines Sekundärstrahls.
Für diesen muß dann der Parameter ![]() bestimmt werden.
Wird das eben geschnittene Objekt mit dem neuen Strahl geschnitten,
hat
bestimmt werden.
Wird das eben geschnittene Objekt mit dem neuen Strahl geschnitten,
hat ![]() wegen der begrenzten Rechengenauigkeit oft einen kleinen
Wert ungleich Null.
Dieser falsche Schnittpunkt kann sichtbare Probleme bewirken.
wegen der begrenzten Rechengenauigkeit oft einen kleinen
Wert ungleich Null.
Dieser falsche Schnittpunkt kann sichtbare Probleme bewirken.