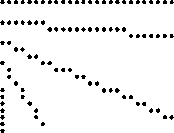Bresenham-Algorithmus

Wir werden zunächst den Fall diskutieren, bei dem die Steigung in $\left [ 0;1 \right ]$ liegt und später verallgemeinern.

Wie oben erwähnt, weicht die gezeichnete Linie für gewöhnlich von der idealen Linie ab:

Abbildung 3.1: Fehler als Abweichung von der Ideal-Linie

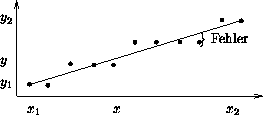
Die Größe dieser Abweichung läßt sich ausnutzen, um zu entscheiden, ob man für die nächste $x$-Koordinate die aktuelle $y$-Koordinate beibehalten kann oder ob man die $y$-Koordinate um $1$ erhöhen muß. Diese Art der Implementation ist aus dem Jahr 1965 und stammt von Jack Bresenham. Der Algorithmus berechnet den jeweils nächsten $y$-Wert aus dem vorherigen und hält dabei den momentanen Fehler nach.

public void drawBresenhamLine1(CGCanvas cgc) {
  int x, y, dx, dy;
  double s, error;

  dy    = y2 - y1;                               // Hoehenzuwachs berechnen
  dx    = x2 - x1;                               // Schrittweite

  x = x1;                                        // Koordinaten retten
  y = y1;
    
  error = 0.0;                                   // momentaner Fehler
  s     = (double) dy / (double) dx;             // Steigung

  while (x <= x2) {                              // fuer jede x-Koordinate
    cgc.setPixel(x, y);                          // setze Pixel
    x++;                                         // naechste x-Koordinate
    error += s;                                  // Fehler aktualisieren
    if (error > 0.5) {                           // naechste Zeile erreicht?
      y++;                                       // neue y-Koordinate
      error-- ;                                  // Fehler anpassen
    }
  }
}

Man kann die verbleibende Gleitkommaarithmetik vermeiden, indem man zur Fehlerbestimmung und zur Entscheidung, ob die $y$-Koordinate angepasst werden muß, eine zweite (wesentlich steilere) Gerade verwendet. Die Steigung dieser neuen Geraden berechnet sich folgendermaßen:

$$s_{neu} = s_{alt} \cdot 2 dx = \frac{dy}{dx}\cdot 2dx = 2dy$$

Für ein ganzzahliges $s$ würde bereits die Multiplikation mit $dx$ genügen. Da wir aber auch den Fahler ganzzahlig machen wollen, müssen wir zusätzlich mit $2$ multiplizieren:

public void drawBresenhamLine2(CGCanvas cgc) {
  int x, y, dx, dy, error, delta;

  dy    = y2 - y1;                               // Hoehenzuwachs berechnen
  dx    = x2 - x1;                               // Schrittweite

  x = x1;                                        // Koordinaten retten
  y = y1;
    
  error = 0;                                     // momentaner Fehler
  delta = 2*dy;                                  // 'Steigung'

  while (x <= x2) {                              // fuer jede x-Koordinate
    cgc.setPixel(x, y);                          // setze Pixel
    x++;                                         // naechste x-Koordinate
    error += delta;                              // Fehler aktualisieren
    if (error > dx) {                            // naechste Zeile erreicht?
      y++;                                       // neue y-Koordinate
      error -= 2*dx;                             // Fehler anpassen
    }
  }
}

Um nochmals etwas Zeit zu sparen, vergleichen wir error mit 0 und verwenden die Abkürzung schritt für -2*dx:

public void drawBresenhamLine3(CGCanvas cgc) {
  int x, y, dx, dy, error, delta, schritt;

  dy    = y2 - y1;                               // Hoehenzuwachs berechnen
  dx    = x2 - x1;                               // Schrittweite

  x = x1;                                        // Koordinaten retten
  y = y1;
    
  error = -dx;                                   // momentaner Fehler
  delta = 2*dy;                                  // 'Steigung'
  schritt = -2*dx;                               // Fehlerschrittweite

  while (x <= x2) {                              // fuer jede x-Koordinate
    cgc.setPixel(x, y);                          // setze Pixel
    x++;                                         // naechste x-Koordinate
    error += delta;                              // Fehler aktualisieren
    if (error > 0) {                             // naechste Zeile erreicht?
      y++;                                       // neue y-Koordinate
      error += schritt;                          // Fehler anpassen
    }
  }
}

Geraden in den anderen 7 Oktanten (Steigung $\notin \left [ 0;1 \right ]$) müssen durch Spiegelung und/oder Vertauschen von $x$ und $y$ auf den 1. Oktanten zurückgeführt werden (siehe folgendes Listing).

Abbildung 3.2: Vom Bresenham-Algorithmus erzeugte Linien

Bresenham-Algorithmus

Beispiel als Applet