Konvexität

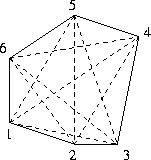
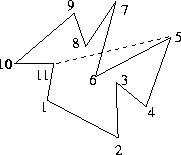
Wir unterscheiden konvexe und konkave Polygone. Bei einem konvexen Polygon ist jeder Eckpunkt von jedem Eckpunkt aus ''sichtbar''. D.h. daß die Verbindungslinie zwischen zwei beliebigen Eckpunkten innerhalb des Polygons verläuft (bei benachbarten Eckpunkten ist diese Verbindungslinie natürlich identisch mit eine Polygonkante). Beim konkaven Polygon schneidet mindestens eine Verbindungslinie mindestens eine Polygonkante:

Konvexes Polygon; alle Verbindungen verlaufen innerhalb des Polygons oder auf dem Rand.

Konkaves Polygon; z.B. die Verbindung zwischen $5$ und $11$ schneidet die Polygonkanten.

Diese visuelle Bestimmung der Konvexität ist sehr aufwändig zu implementieren. Einfacher ist der Algorithmus von Paul Bourke, dessen Idee so veranschaulicht werden kann: ''Wenn man mit dem Fahrrad die Aussenkanten des Polygons entlangfährt und dabei nur nach links oder nur nach rechts lenken muß, ist das Polygon konvex. Wenn man zwischendurch mal die Lenkrichtung wechseln muß, dann ist es konkav. Dabei ist es egal, ob man im Uhrzeigersinn oder gegen den Uhrzeigersinn die Kanten abfährt.''

Um festzustellen, ob der nächste Punkt von der aktuellen Polygonkante aus gesehen links oder rechts liegt, benutzen wir die Geradengleichung in der Normalenform, die sich aus der parametrisierten Geradengleichung ergibt, wenn man den Parameter $r$ eliminiert:

$$F(u) = u_x \cdot v_y - u_y \cdot v_x + (v_x \cdot p_y - v_y \cdot p_x)$$

Es gilt:

$$\begin{eqnarray*} F(u)&=&0\mbox{ f\uml {u}r } u \mbox{ auf der Geraden.}\\ F(u)... ...n.}\\ F(u)&>&0\mbox{ f\uml {u}r } u \mbox{ rechts der Geraden.} \end{eqnarray*}$$

''links'' und ''rechts'' sind dabei in der Richtung von $\vec{v}$ gemeint; d.h. die Seite wechselt, wenn man den Umlaufsinn des Polygons tauscht.

Es muß nur für jedes Punktepaar die Geradengleichung aufgestellt und der darauffolgende Punkt eingesetzt werden. Sobald einmal ein Wert herauskommt, der im Vorzeichen von den bisherigen Werten abweicht, ist das Polygon als konkav identifiziert und es brauchen keine weiteren Punkte mehr getestet zu werden. Wenn sich fuer alle Punkte immer das gleiche Vorzeichen ergibt, dann ist das Polygon konvex.