Umlaufszahl

Bei dieser Methode wird gezählt, wie oft die Begrenzungskurve den Punkt $P$ ganz umläuft. D.h. die Umlaufszahl (oder Winding Number) $i$ liegt in $\mathbb{N}$ für Punkte, die im Polygon liegen und ist $0$ für Punkte, die nicht im Polygon liegen.

Für jede Polygonkante von $P_i$ nach $P_{i+1}$ bildet man die Vektoren von $P$ nach $P_i$ und von $P$ nach $P_{i+1}$ und berechnet den Winkel $\Theta_i$ zwischen diesen beiden Vektoren. Die Umlaufszahl ergibt sich dann zu:

$$wn = \frac{1}{2\pi} \sum_{i=0}^{n-1} \Theta_i$$

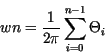
Diese Methode ist jedoch mathematisch aufwändig. Es reicht, wenn der Algorithmus zählt, wie oft die Begrenzungskurve an einem bestimmten Punkt vorbeikommt. Es wird also wieder ein Strahl von $P$ waagerecht nach rechts geschossen und wieder wird die Zahl der Kanten ermittelt, die diesen Strahl schneiden. Allerdings wird jetzt die Richtung der Kante berüecksichtigt. Wenn die Kante von unten nach oben läuft, wird die Umlaufszahl um 1 erhöht. Wenn die Kante hingegen von oben nach unten läuft, wird die Umlaufszahl um 1 erniedrigt. Dadurch erhalten Punkte außerhalb des Polygons die Umlaufszahl 0 und innere Punkte eine Umlaufszahl ungleich 0.

public boolean contains(int x, int y) {
  int wn = 0;

  int x1 = xpoints[npoints-1];
  int y1 = ypoints[npoints-1];
  int x2 = xpoints[0];
  int y2 = ypoints[0];
 
  boolean startUeber = y1 >= y? true : false;
  for(int i = 1; i<npoints ; i++) {
    boolean endUeber = y2 >= y? true : false;
    if(startUeber != endUeber) {
      if((y2 - y)*(x2 - x1) <= (y2 - y1)*(x2 - x)) {
        if(endUeber) {
          wn ++;
        }
      }
      else {
        if(!endUeber) {
          wn --;
        }
      }
    }

    startUeber = endUeber;
    y1 = y2;
    x1 = x2;
    x2 = xpoints[i];
    y2 = ypoints[i];
  }
  return wn == 0;
}