beschreibt.
Projiziere den ![]() -Würfel längs der Weiß-Schwarz-Diagonale
(Abbildung
8.8
).
-Würfel längs der Weiß-Schwarz-Diagonale
(Abbildung
8.8
).
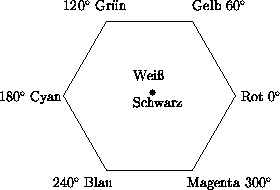
Dieses Sechseck bildet die Basis einer Pyramide.
Die Wahl des Farbtons (hue) geschieht durch
Angabe eines Winkels (![]() Rot).
Rot).
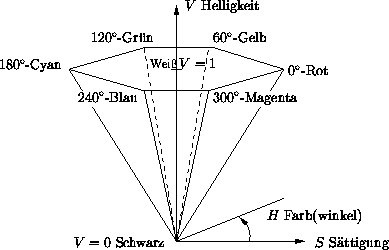
Der Parameter ![]() liegt zwischen
liegt zwischen ![]() und
und ![]() und bestimmt die
Intensität der Farbe (dargestellt durch die Senkrechte).
Der Parameter
und bestimmt die
Intensität der Farbe (dargestellt durch die Senkrechte).
Der Parameter ![]() liegt zwischen
liegt zwischen ![]() und
und ![]() und bestimmt die Reinheit
der Farbe (Entfernung von der Senkrechten).
Die Farbselektion kann erfolgen, indem z.B. zunächst eine reine
Farbe ausgewählt wird
(
und bestimmt die Reinheit
der Farbe (Entfernung von der Senkrechten).
Die Farbselektion kann erfolgen, indem z.B. zunächst eine reine
Farbe ausgewählt wird
(
![]() ).
Das Hinzumischen von Weiß zur Erzeugung von Pastellfarben erfolgt durch
Reduktion von
).
Das Hinzumischen von Weiß zur Erzeugung von Pastellfarben erfolgt durch
Reduktion von ![]() bei konstantem
bei konstantem ![]() .
Das Hinzumischen von Schwarz
(zur Erzeugung von dunklen Farben) erfolgt durch Reduktion von
.
Das Hinzumischen von Schwarz
(zur Erzeugung von dunklen Farben) erfolgt durch Reduktion von ![]() bei
konstantem
bei
konstantem ![]() .
.
Umrechnung von ![]() nach
nach ![]()
Die Achse ![]() entspricht der Diagonalen im
entspricht der Diagonalen im ![]() -Würfel
durch die Punkte Schwarz und Weiß,
deshalb ist der Wert für
-Würfel
durch die Punkte Schwarz und Weiß,
deshalb ist der Wert für ![]() gleich dem Maximum der
gleich dem Maximum der ![]() -Intensitäten.
Die Werte
-Intensitäten.
Die Werte ![]() und
und ![]() können aus der Position des Punktes in jenem Sechseck berechnet werden,
das durch Projektion des kleinsten, den
können aus der Position des Punktes in jenem Sechseck berechnet werden,
das durch Projektion des kleinsten, den ![]() -Punkt beinhaltenden Würfels erzeugt wird.
-Punkt beinhaltenden Würfels erzeugt wird.
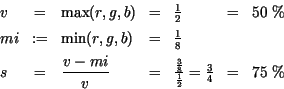
Umrechnung von ![]() nach
nach ![]()
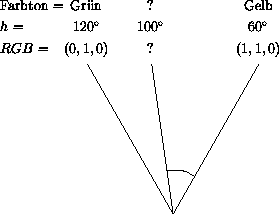
| = | Winkel/60 | - | Winkel div 60 | |||
| = | - | 1 | = | |||
| Farbton |
: | für |
|||||||
| Sättigung |
: |
|
für |
||||||
| Helligkeit |
: |
|
für |
||||||
| Lösung: | 64 | 128 | 32 |