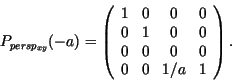Die abgebildeten Objekte werden proportional zu ihrem Abstand zur
Bildebene verkleinert.
Je nachdem, ob die Bildebene eine, zwei oder
drei der Koordinatenachsen schneidet, entstehen ein, zwei oder
drei Fluchtpunkte.
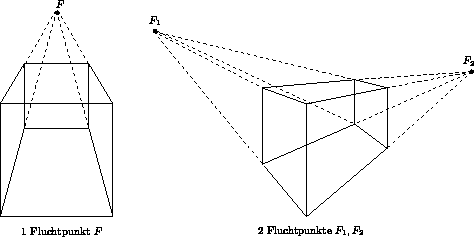
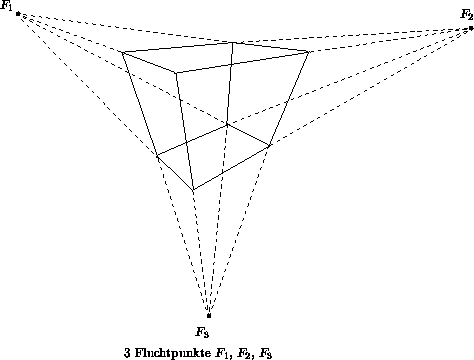
Abbildung
12.2: Zentralprojektionen mit unterschiedlich vielen Fluchtpunkten
OBdA sei die Bildebene gleich der 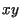 -Ebene,
und das Projektionszentrum liege auf der negativen
-Ebene,
und das Projektionszentrum liege auf der negativen 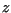 -Achse im
Punkt
-Achse im
Punkt 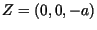 .
Gegeben Punkt
.
Gegeben Punkt 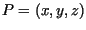 .
Gesucht sind auf der Bildebene die Koordinaten des projizierten
Bildpunktes
.
Gesucht sind auf der Bildebene die Koordinaten des projizierten
Bildpunktes
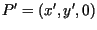 .
.
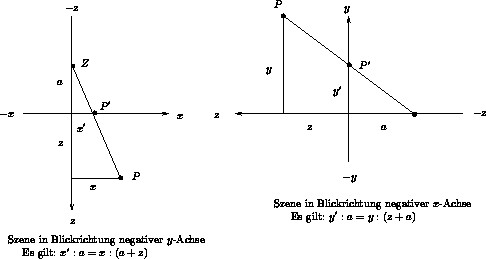
Abbildung
12.3: Anwendung der Strahlensätze
Betrachtet man die Szene ``von oben'' und ``von der Seite'',
so erhält man aufgrund der Strahlensätze die Beziehung
Die homogenen Koordinaten des projizierten Punktes lauten
Für die Transformationsmatrix der perspektivischen
Projektion ergibt sich also:







![]() -Ebene,
und das Projektionszentrum liege auf der negativen
-Ebene,
und das Projektionszentrum liege auf der negativen ![]() -Achse im
Punkt
-Achse im
Punkt ![]() .
Gegeben Punkt
.
Gegeben Punkt ![]() .
Gesucht sind auf der Bildebene die Koordinaten des projizierten
Bildpunktes
.
Gesucht sind auf der Bildebene die Koordinaten des projizierten
Bildpunktes
![]() .
.