Für einen Punkt ![]() sei
sei
![]()
Es gilt:
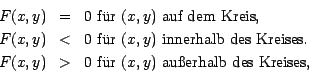
Verwende ![]() als Entscheidungsvariable dafür, ob
als Entscheidungsvariable dafür, ob
![]() erniedrigt werden muß, wenn
erniedrigt werden muß, wenn ![]() erhöht wird.
erhöht wird.
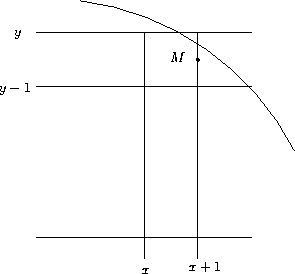
![]() wird angewendet auf die Mitte
wird angewendet auf die Mitte ![]() zwischen Zeile
zwischen Zeile ![]() und
und ![]() (siehe Abbildung
3.6
).
(siehe Abbildung
3.6
).
![]()
| Falls |
|
|
|
|
| Idee: | Entscheide anhand von |
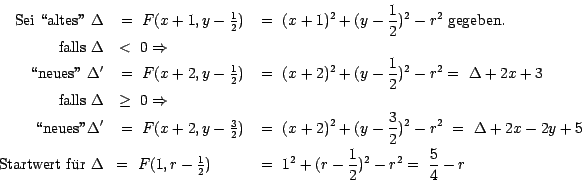
Also ergibt sich:
public void drawBresenhamCircle1(CGCanvas cgc) {
int xh, yh;
double delta;
xh = 0; // Koordinaten retten
yh = r;
delta = 5.0/4.0 - r;
while(yh >= xh) { // Fuer jede x-Koordinate
cgc.setPixel(xh, yh); // Pixel im 2. Oktanden setzen
if (delta < 0.0) { // Falls noch im Kreis
delta+=2*xh + 3.0; // Abweichung aktualisieren
xh++; // naechste x-Koordinate
}
else { // aus dem Kreis gelaufen
delta+=2*xh - 2*yh + 5.0; // Abweichung aktualisieren
xh++; // naechste x-Koordinate
yh--; // naechste y-Koordinate
}
}
}
Substituiere delta durch d := delta - 1/4.
Dann ergibt sich
als neue Startbedingung: d := 5/4 - r - 1/4 = 1 - r
als neue if-Bedingung: if (d < 0)
Da d
nur ganzzahlige Werte annimmt, reicht der Vergleich mit 0.
Weitere Verbesserung:
Ersetze 2xh + 3 durch dx mit Initialwert dx = 3;
Ersetze 2xh - 2yh + 5 durch dxy mit Initialwert
dxy = -2*r + 5
Es ergibt sich:
public void drawBresenhamCircle2(CGCanvas cgc) {
int xh, yh, d, dx, dxy;
xh = 0; // Koordinaten retten
yh = r;
d = 1 - r; // Startbedingung einstellen
dx = 3;
dxy = -2*r + 5;
while(yh >= xh) { // Fuer jede x-Koordinate
cgc.setPixel(xh, yh); // Pixel im 2. Oktanden setzen
if (d < 0) { // Falls noch im Kreis
d += dx; dx += 2; dxy += 2; xh++; // Entscheidungsvariablen setzen
}
else {
d +=dxy; dx += 2; dxy += 4; xh++; yh--;// Entscheidungsvariablen setzen
}
}
}
Um den ganzen Kreis zu zeichnen, wird die Symmetrie zum Mittelpunkt ausgenutzt.
Die Anzahl der erzeugten Punkte des Bresenham-Algorithmus für den vollen Kreis
beträgt
![]() Punkte.
Verglichen mit dem Kreisumfang von
Punkte.
Verglichen mit dem Kreisumfang von
![]() liegt dieser Wert um 10% zu tief.
liegt dieser Wert um 10% zu tief.
public void draw(CGCanvas cgc) {
int xh, yh, d, dx, dxy;
xh = 0; // Koordinaten retten
yh = r;
d = 1-r;
dx = 3;
dxy = -2*r + 5;
while(yh >= xh) { // Fuer jede x-Koordinate
cgc.setPixel(x+xh, y+yh); // alle 8 Oktanden werden
cgc.setPixel(x+yh, y+xh); // gleichzeitig gesetzt
cgc.setPixel(x+yh, y-xh);
cgc.setPixel(x+xh, y-yh);
cgc.setPixel(x-xh, y-yh);
cgc.setPixel(x-yh, y-xh);
cgc.setPixel(x-yh, y+xh);
cgc.setPixel(x-xh, y+yh);
if (d < 0) { // Falls noch im Kreis
d+=dx; dx+=2; dxy+=2; xh++; // passend aktualisieren
}
else { // Aus dem Kreis gelaufen
d+=dxy; dx+=2; dxy+=4; xh++; yh--; // passend aktualisieren
}
}
}

Demonstration der Laufzeitunterschiede