Punkt in Polygon

Wenn der Benutzer mit der Maus auf dem Bildschirm in ein Polygon klickt, damit es anschließend gefüllt wird, so muß zunächst festgestellt werden, in welches Polygon geklickt wurde, damit einer der oben beschriebenen Algorithmen mit dem Füllen beginnen kann.

Nach dem Jordanschen Kurvensatz zerlegt jede einfache geschlossene Kurve die 2D-Ebene in genau zwei durch die Kurve verbundene Gebiete: Ein beschränktes Inneres und ein unbeschränktes Äußeres. Deshalb bedeutet eine Kreuzung mit der Kurve einen Wechsel von einem Gebiet in das andere.

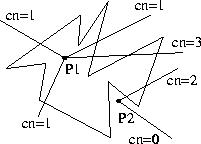
Da ein einfaches Polygon eine Kurve im o.g. Sinne ist, gilt entsprechend, daß ein Punkt genau dann im Inneren des Polygons liegt, wenn ein von ihm in eine beliebige Richtung ausgehender Strahl ungeradzahlig viele Polygonkanten kreuzt, also die Kreuzungszahl (oder Crossing Number) ungerade ist (Abbildung 4.4 a)). Diese Idee ist auch als Paritäts- oder Gerade-Ungerade-Test bekannt.

Ermittlung der Kreuzungszahl (cn) mit einem Teststrahl

a) Polygon mit zwei Testpunkten. P1 liegt im Polygon (cn ungerade); P2 nicht (cn gerade).

b) Zur effizienteren Berechnung wird der Teststrahl waagerecht nach rechts geschossen.

Es muß für jede Polygonkante ermittelt werden, ob der Strahl sie schneidet. Wenn ja, wird die Kreuzungszahl um 1 erhöht, sonst nicht.

Dazu wird vom Testpunkt $P$ der Strahl waagerecht nach rechts geschossen (Abbildung 4.4 b).

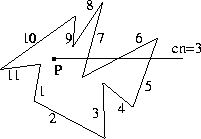
Um den Aufwand für die Schnittpunktberechnung auf diejenigen Kanten zu reduzieren, die den Strahl wirklich schneiden, werden zunächst einige Tests bezüglich der Koordinaten durchgeführt. Wenn Anfangs- und Endpunkt der aktuellen Polygonkante beide oberhalb oder beide unterhalb der Strahls liegen, kann die Kante den Strahl nicht schneiden (z.B. Kanten 1, 2, 3, 4, 8, 9, 11 in Abbildung 4.4 b)). Wenn ein Punkt oberhalb und der andere unterhalb liegt, kann ein Schnittpunkt vorliegen und die $x$-Koordinaten werden untersucht. Sind beide Punkte rechts von $P$, schneidet der Strahl die Kante irgendwo (diese Information ist ausreichend) und die Kreuzungszahl wird erhöht (Kanten 7, 6, 5). Sind beide links von $P$ gibt es keinen Schnittpunkt. Ist einer links und einer rechts von $P$ muß berechnet werden, wo die Kante den $y$-Wert von $P$ erreicht; d.h. ob der Schnittpunkt rechts von $P$ liegt (z.B. Kante 7). Wenn ja, wird die Kreuzungszahl erhöht.

Ein Problem stellen die bereits beim ScanLine-Verfahren erwähnten Sonderfälle dar, bei denen der Strahl genau einen Polygonpunkt trifft.

Ein Sonderfall liegt immer dann vor, wenn der Strahl einen oder mehrere Polygonpunkte trifft.

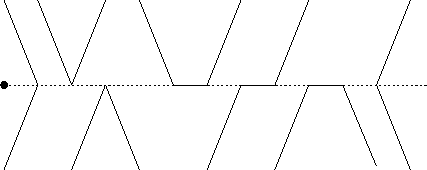
Das Problem wird gelöst, indem so getan wird als läge der Polygonpunkt infinitesimal üeber dem Strahl. Bei der Implementation wird dies dadurch erreicht, daß Polygonpunkte mit einem $y$-Wert $\geq p_y$ als über dem Strahl liegend interpretiert werden. Auf diese Weise wird gleichzeitig die Frage geklärt, zu welchem Polygon ein Pixel gehört, wenn zwei Polygone eine (oder mehrere) identische Kanten haben.

Damit ergibt sich folgender Algorithmus:

public boolean contains(int x, int y) {
  boolean inside = false;

  int x1 = xpoints[npoints-1];
  int y1 = ypoints[npoints-1];
  int x2 = xpoints[0];
  int y2 = ypoints[0];
 
  boolean startUeber = y1 >= y? true : false;
  for(int i = 1; i<npoints ; i++) {
    boolean endUeber = y2 >= y? true : false;
    if(startUeber != endUeber) {
      if((double)(y*(x2 - x1) -y1*x2 +y2*x1)/(double)(y2-y1) >= x) {
        inside = !inside;
      }
    }
    startUeber = endUeber;
    y1 = y2;
    x1 = x2;
    x2 = xpoints[i];
    y2 = ypoints[i];
  }

  return inside;
}

Die Division zur Berechnung des Schnittpunktes kann vermieden werden, wenn man die Steigung der Polygonkante mit der Steigung der Geraden durch $P$ und den Endpunkt der Kante vergleicht und dabei berücksichtigt, ob der Endpunkt eine größere oder eine kleinere $y$-Koordinate hat.

public boolean contains(int x, int y) {
  boolean inside = false;

  int x1 = xpoints[npoints-1];
  int y1 = ypoints[npoints-1];
  int x2 = xpoints[0];
  int y2 = ypoints[0];
 
  boolean startUeber = y1 >= y? true : false;
  for(int i = 1; i<npoints ; i++) {
    boolean endUeber = y2 >= y? true : false;
    if(startUeber != endUeber) {
      if((y2 - y)*(x2 - x1) <= (y2 - y1)*(x2 - x)) {
        if(endUeber) {
          inside = !inside;
        }
      }
      else {
        if(!endUeber) {
          inside = !inside;
        }
      }
    }

    startUeber = endUeber;
    y1 = y2;
    x1 = x2;
    x2 = xpoints[i];
    y2 = ypoints[i];
  }
  return inside;
}