NURBS

Über die Eigenschaften der B-Splines hinaus, wäre für den 3D-Fall auch eine Invarianz unter projektiven Abbildungen wünschenswert, da dort die 3D-Kurven auf den 2D-Bildschirm projeziert werden müssen.

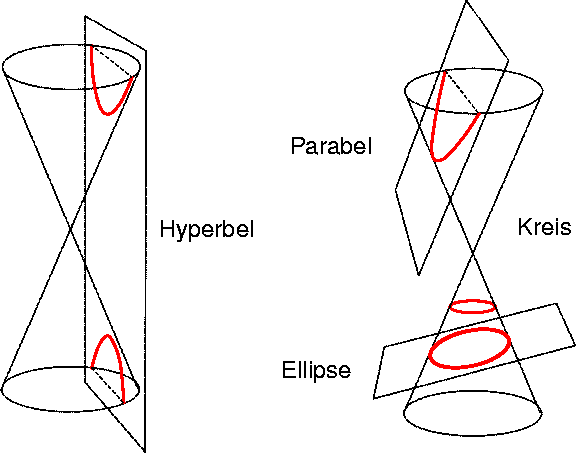
Um möglichst große Freiheit bei den darzustellenden Formen zu haben, sollten die Kurven beliebige Kegelschnitte (also Kreise, Parabeln und Hyperbeln) annähern können, wie sie in Abbildung 7.7 gezeigt werden.

Abbildung 7.7: Kreis, Ellipse, Parabel und Hyperbel erzeugt durch Kegelschnitte

Beide Wünsche werden von der allgemeinsten Form zum Zeichnen von Kurven erfüllt. Es handelt sich dabei um NURBS (nonuniform rational basis splines).

$$P(t) = \sum_{i=0}^n R_{i,k}(t) \cdot P_i ~~~{\rm mit}$$

$$R_{i,k}(t) = \frac{h_i \cdot N_{i,k}(t)}{\sum_{j=0}^n h_j \cdot N_{j,k}(t)}$$

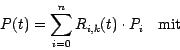
Nonuniform bedeutet, dass die Knoten auf dem Knotenvektor nicht äquidistant sein müssen; rational bedeutet, dass die Gewichtung eines Kontrollpunktes durch den Quotienten zweier Polynome definiert wird.

Abbildung 7.8: Einfluss des Gewichtes auf den Verlauf der Kurve

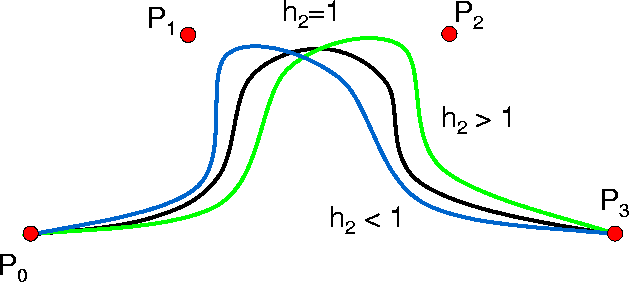
Abbildung 7.8 zeigt den Einfluss der Gewichte auf den Verlauf der Kurve. Ein Gewicht $h_2 > 1$ verschiebt die Kurve in Richtung Kontrollpunkt $P_2$, ein Gewicht $h_2 < 1$ verringert den Einfluss von Kontrollpunkt $P_2$ (und erhöht dadurch den Einfluss von Kontrollpunkt $P_1$.

Zur Berechnung von NURBS-Kurven bedient man sich der homogenen Koordinaten: Zunächst wird ein Punkt $P_i(x_i,y_i)^T$ in seine homogenen Koordinaten $P(x_i,y_i,1)^T$ überführt und dann mit seinem Gewicht $h_i$ multipliziert. Die so entstandenen Punkte $P'_i(w_i\cdot x_i, w_i \cdot y_i, h_i)^T$ werden nun mit den Gewichtspolynomen $N_{i,k}$ verarbeitet: $P'(t) = \sum_{i=0}^n N_{i,k}(t) \cdot P_i'$

Zur Anzeige der errechneten Kurve werden die homogenen Koordinaten durch Division der dritten Komponente in Punktkoordinaten überführt:

$$(x,y,z)^T \rightarrow (\frac{x}{z}, \frac{y}{z})^T$$

NURBS bieten gegenüber B-Splines einige Vorteile:

• NURBS sind eine Verallgemeinerung der B-Splines. Für $h_i = 1 ~~\forall i$ reduziert sich die NURBS-Kurve zur entsprechenden B-Spline-Kurve.

• NURBS sind invariant bzgl. perspektivischer Projektion. Dies bedeutet, daß zur Projektion einer Kurve nicht alle Kurvenpunkte projeziert werden müssen, sondern es reicht, die Stützpunkte zu projezieren und dann zu einer Kurve zu verbinden.

• NURBS sind (im Gegensatz zu nicht-rationalen B-Splines) in der Lage, Kreise zu beschreiben. Abbildung 7.9 zeigt die 8 Kontrollpunkte zusammen mit ihren Gewichten für den Einheitskreis mit Radius 1. Der zugehörige Knotenvektor lautet (0,0,1,1,2,2,3,3,4,4), wobei der erste und der letzte Kontrollpunkt jeweils doppelt benutzt werden.

Abbildung 7.9: Kreis erzeugt durch NURBS