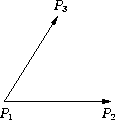
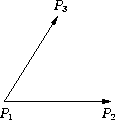
Der Vektor
![]() bildet den
Normalenvektor zur Fläche.
bildet den
Normalenvektor zur Fläche.
Ist eine Ebene durch ihre Ebenengleichung
![]() gegeben, so ergibt sich der
Normalenvektor als
gegeben, so ergibt sich der
Normalenvektor als
![]() .
.
Ist ein Normalenvektor
![]() gegeben, so errechnet sich
gegeben, so errechnet sich ![]() durch
Einsetzen eines beliebigen Punktes der Ebene.
durch
Einsetzen eines beliebigen Punktes der Ebene.
Ein Punkt ![]() liegt
liegt
| oberhalb der Ebene, | falls | |
| unterhalb der Ebene, | falls | |
| in der Ebene, | falls |
Wir werden jede ebene Fläche als Ausschnitt einer Ebene ansehen und dem
entsprechenden Polygon eine Flächennormale ![]() zuweisen.
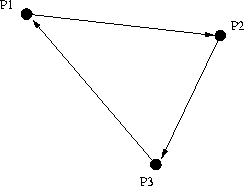
Der Umlaufsinn des Polygons entscheidet, in welche
Richtung die Flächennormale weist:
zuweisen.
Der Umlaufsinn des Polygons entscheidet, in welche
Richtung die Flächennormale weist:
|
|
ObdA werden der erste, der zweite und der letzte Punkt eines Polygons zur Bestimmung der Normalen herangezogen. Im Fall eines im Uhrzeigersinn (clockwise) orientierten Polygons ergibt sich:
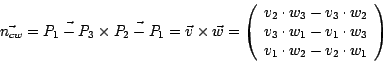
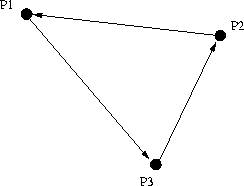
Falls das Polygon gegen den Uhrzeigersinn (counter clockwise) orientiert ist, tauschen die
Vektoren ![]() und
und ![]() die Plätze:
die Plätze:
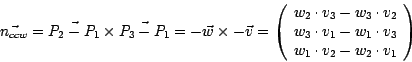
Es gilt also:
Die beiden Normalen weisen in entgegengesetzte Richtungen (Schiefsymmetrie des Kreuzproduktes).
Wir werden alle Polygone gegen den Uhrzeigersinn orientieren. Für konvexe Polygone gilt dann: Die Normale einer Fläche, die man so betrachtet, daß sie gegen den Uhrzeigersinn orientiert ist, zeigt in Richtung des Betrachters. Man ''sieht'' die Seite der Fläche, die die ''Außenseite'' sein soll.
Das Kreuzprodukt ist linear in jedem Argument. Es ist weder kommutativ
(s.o.) noch assoziativ (
![]() ).
).