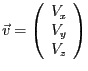Aufgabe 7.4 (35 Punkte)

Gegeben sei ein Vektor $\vec{v} = \left ( \begin{array}{c} V_x \\ V_y \\ V_z \end{array} \right )$ und der Punkt $P=(P_x,P_y,P_z)$. Gesucht ist die Gesamtmatrix, die den Punkt $P$ um die Achse, die durch den Ursprung des Koordinatensystems und den Vektor $\vec{v}$ definiert ist, um den Winkel $\gamma$ dreht.

Ihre Transformationssequenz soll auf einer Drehung um die y-Achse basieren. Hinweis: Transformieren Sie also zunächst die Drehachse auf die y-Achse.

Schreiben Sie jede Teiltransformation als Matrix auf, geben Sie schriftlich eine kurze Erläuterung zu jedem Schritt.

Wenden Sie Ihre Ergebnismatrix schließlich an. Rotieren Sie dazu den Punkt $(1,2,3)$ um $90^{\circ}$ um die Drehachse, die durch den Punkt $(1,-1,1)$ und den Koordinatenursprung verläuft. Geben Sie Ihre Gesamtrotationsmatrix und die Koordinaten des transformierten Punktes an.

Musterlösung vom 02.06.2010:
Um eine Rotation um die durch $\vec{v}$ und dem Ursprung des Koordinatensystems definierte Achse durchzuführen, sind folgende Schritte notwendig:

1. Rotation des Vektors $\vec{v}$ um die x-Achse, so dass der Vektor sich in der xy-Ebene befindet
   Der Rotationsvektor muss um den Winkel $\alpha$ in die xy-Ebene gedreht werden. Der Winkel $\alpha$ muss nicht errechnet werden. Er kann über das Seitenverhältnis der Wert für Sinus, bzw Cosinus angegeben werden. Hinweis: Es wird angenommen, dass der Vektor $\vec{v}$ bereits normiert wurde, damit in Schritt 2 die angegebene Vereinfachung vorgenommen werden kann.

   Sei $d_1=\sqrt{{v_y}^2+{v_z}^2}$. Dann folgt $\sin{\alpha} = \frac{v_z}{d_1}$ und $\cos{\alpha}=\frac{v_y}{d_1}$, wobei $d_1 \ne 0$.

   Diese Werte können in die Rotationsmatrix eingetragen werden, wobei zu beachten ist, dass bei der Veranschaulichung der sin- und cos-Zusammenhänge die x-Achse vom Betrachter weg zeigt, blickt man auf die yz-Ebene. Mit anderen Worten muss, um diese Zusammenhänge nutzen zu können, um den Winkel $-\alpha$ gedreht werden, also mit dem Uhrzeigersinn. Da $sin(-\alpha) = -sin(\alpha)$ und $cos(-\alpha) = cos(\alpha)$ ergibt sich:

   
   

   $$R_x(-\alpha) = \left [ \begin{array}{rrrr} 1 & 0 & 0 & 0\\ ... ... \frac{v_y}{d_1} & 0\\ 0 & 0 & 0 & 1\\ \end{array} \right ]$$
   
   

   Der Rotationsvektor liegt nach Ausführung dieser Transformation in der yx-Ebene.

2. Rotation des Vektors $\vec{v}$ um die z-Achse, so dass der Vektor mit der y-Achse identisch ist
   Der Winkel $\beta$, um den der Vektor $\vec{v}$ um die x-Achse gedreht werden mus, braucht ebenfalls nicht ausgerechnet zu werden. Die Werte der Seitenverhältnisse werden direkt für $\sin{\beta}$ und $\cos{\beta}$ in die Matrix eingetragen.

   Die Länge der Hypotenuse ist $d_2=\sqrt{d_1^2+{v_x}^2}=\sqrt{{v_x}^2+{v_y}^2+{v_z}^2}=\vert\vec{v}\vert=1$. Hier nutzen wir die vorgenommene Normierung aus. Daraus folgt $\sin{\beta}=v_x$ und $\cos{\beta}=d_1$.

   Diese Werte können direkt in die Matrix übernommen werden, da die Rotation gegen den Uhrzeigersinn erfolgt.

   
   

   $$R_z(\beta) = \left [ \begin{array}{rrrr} \sqrt{{v_y}^2+{v_z}... ... 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{array} \right ]$$
   
   

   Der Rotationsvektor liegt nun auf der y-Achse.

3. Rotation des Objektes um die y-Achse mit dem vorgegebenen Winkel
   Hier werden die trigonometrischen Funktionen benötigt. Die Rotation um die y-Achse lautet:

   
   

   $$R_y(\gamma) = \left [ \begin{array}{rrrr} \cos{\gamma} & 0 &... ... 0& \cos{\gamma} & 0\\ 0 & 0 & 0 & 1\\ \end{array} \right ]$$
   
   

4. Inverse Transformation zu Schritt 2
   Der Rotationsvektor wird mit dem Winkel $-\beta$ um die z-Achse zurück rotiert. Dazu müssen lediglich die Vorzeichen der Einträge der Matrix $R_z$ bei den Sinuswerten getauscht werden.

   
   

   $$R_z(-\beta) = \left [ \begin{array}{rrrr} \sqrt{{v_y}^2+{v_z... ... 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{array} \right ]$$
   
   

5. Inverse Transformation aus Schritt 1
   Der Rotationsvektor $\vec{v}$ wird mit dem Winkel $\alpha$ um die x-Achse zurückrotiert:

   
   

   $$R_x(\alpha) = \left [ \begin{array}{rrrr} 1 & 0 & 0 & 0\\ ... ... \frac{v_y}{d_1} & 0\\ 0 & 0 & 0 & 1\\ \end{array} \right ]$$
   
   

Die Gesamtmatrix für die Rotation um eine beliebige durch den Ursprung gehende Achse erhält man durch Mutiplikation der einzelnen Matrizen. Wenn die Rotationsachse nicht durch den Ursprung des Koordinatensystems verläuft, ist zusätzlich eine Multiplikation mit den entsprechenden Translationsmatrizen notwendig. Außerdem ist zu bemerken, dass das Verfahren alternativ auch so umgesetzt werden kann, dass zunächst um die z-Achse in die xy-Ebene rotiert wird und danach um die x-Achse in die y-Achse. Das Ergebnis ist dabei das gleiche.

Angewandt auf den angegebenen Punkt und die Achse ergibt sich die (numerisch notierte) Gesamtrotationsmatrix:

$$R(90^{\circ}) = \left [ \begin{array}{rrrr} 0.333 & -0.911 &... ... & 0.244 & 0.333 & 0\\ 0 & 0 & 0 & 1\\ \end{array} \right ]$$

sowie der rotierte Punkt mit den neuen (numerisch notierten) Koordinaten $(-2.220, -1.821, 2.399, 1)$