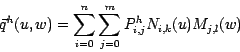
Eine NURBS-Fläche sieht in homogenen Koordinaten folgendermaßen aus:
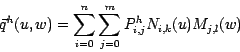
Die ![]() sind die vierdimensionalen homogenen Stützpunkte.
Die
sind die vierdimensionalen homogenen Stützpunkte.
Die ![]() und die
und die
![]() sind die nichtrationalen B-Spline-Basisfunktionen
aus Kapitel 7.
Um affine Koordinaten zu erreichen, wird wieder durch die homogenen
Koordinaten dividiert:
sind die nichtrationalen B-Spline-Basisfunktionen
aus Kapitel 7.
Um affine Koordinaten zu erreichen, wird wieder durch die homogenen
Koordinaten dividiert:
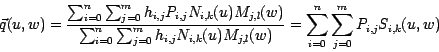
wobei ![]() die dreidimensionalen Stützpunkte sind.
Sie ergeben das Kontrollnetz für die Oberfläche. Bei den
die dreidimensionalen Stützpunkte sind.
Sie ergeben das Kontrollnetz für die Oberfläche. Bei den
![]() handelt es sich um die biparametrisierten
Flächenbasisfunktionen
handelt es sich um die biparametrisierten
Flächenbasisfunktionen
Die ![]() sind nicht das Produkt der
sind nicht das Produkt der ![]() und der
und der
![]() aus Kapitel 7. Sie haben aber ähnliche analytische
Eigenschaften, so daß die NURBS-Fläche ähnliche analytische und
geometrische Eigenschaften, wie die früher erwähnten NURBS-Kurven:
aus Kapitel 7. Sie haben aber ähnliche analytische
Eigenschaften, so daß die NURBS-Fläche ähnliche analytische und
geometrische Eigenschaften, wie die früher erwähnten NURBS-Kurven: