Wenn wir ein Koordinatensystem wählen, um die Punkte des ![]() zu
beschreiben, dann wählen wir damit auch eine Basis, die den Vektorraum
aufspannt. Die Basisvektoren sind die Einheitsvektoren in Richtung der
Koordinatenachsen. Zwei verschiedene Koordinatensysteme haben zwei
verschiedene Basen.
zu
beschreiben, dann wählen wir damit auch eine Basis, die den Vektorraum
aufspannt. Die Basisvektoren sind die Einheitsvektoren in Richtung der
Koordinatenachsen. Zwei verschiedene Koordinatensysteme haben zwei
verschiedene Basen.
Die Transformation von einem Koordinatensystem in ein anderes bedeutet also
einen Basiswechsel.
Gegeben sei ein Koordinatensystem ![]() (z.B. das Kartesische
Koordinatensystem) mit zugehöriger Basis
(z.B. das Kartesische
Koordinatensystem) mit zugehöriger Basis ![]() . Z.B. die
kanonische Basis (in Matrixschreibweise mit Spaltenvektoren):
. Z.B. die
kanonische Basis (in Matrixschreibweise mit Spaltenvektoren):
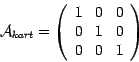
In homogenen Koordinaten werden als vierter Spaltenvektor die
Koordinaten des Ursprungs von Koordinatensystem ![]() , beschrieben bzgl. Basis
, beschrieben bzgl. Basis
![]() (hier also:
(hier also:
![]() ), hinzugenommen:
), hinzugenommen:
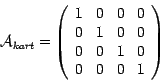
Weiterhin sei ein zweites - von ![]() verschiedenes - Koordinatensystem
verschiedenes - Koordinatensystem ![]() gegeben. Auch dieses Koordinatensystem spezifiziert 4 ausgezeichnete
Elemente: Seinen Ursprungspunkt
gegeben. Auch dieses Koordinatensystem spezifiziert 4 ausgezeichnete
Elemente: Seinen Ursprungspunkt ![]() und die drei Einheitsvektoren
und die drei Einheitsvektoren
![]() ,
, ![]() ,
, ![]() .
.
Diese Elemente lassen sich sowohl bzgl. der Basis ![]() als auch
bzgl. der Basis
als auch
bzgl. der Basis ![]() darstellen. Um von einer Darstellung in die
andere zu kommen, muß die gegebene Darstellung nur mit der im Folgenden
beschriebenen Matrix multipliziert werden.
darstellen. Um von einer Darstellung in die
andere zu kommen, muß die gegebene Darstellung nur mit der im Folgenden
beschriebenen Matrix multipliziert werden.
Wenn man die homogenen Koordinatenvektoren in Spaltenschreibweise nebeneinander
anordnet ergeben sie die Matrix
![]() , die den Übergang von Basis
, die den Übergang von Basis ![]() zur Basis
zur Basis
![]() beschreibt:
beschreibt:

Beispiel (für den 2-dimensionalen Fall):
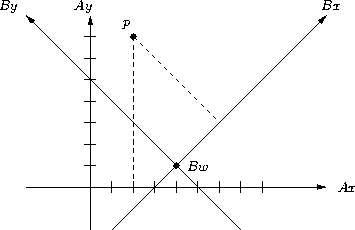
| lautet |
|
||
| lautet |
|
||
| Ursprung: | lautet | ||
| Punkt: |
|
lautet |
|
Der Aufbau der Matrix
![]() repräsentiert die erforderliche Drehung und
Verschiebung, um einen aus der Sicht
von Koordinatensystem
repräsentiert die erforderliche Drehung und
Verschiebung, um einen aus der Sicht
von Koordinatensystem
![]() (also bzgl. Basis
(also bzgl. Basis ![]() beschriebenen Punkt
beschriebenen Punkt ![]() aus der Sicht
von Koordinatensystem
aus der Sicht
von Koordinatensystem ![]() (also bzgl.
(also bzgl. ![]() ) zu
beschreiben. Im zwei-dimensionalen Fall wird
zunächst der Punkt
) zu
beschreiben. Im zwei-dimensionalen Fall wird
zunächst der Punkt ![]() um den Winkel
um den Winkel ![]() gedreht,
der sich zwischen den Achsen der Koordinatensysteme
gedreht,
der sich zwischen den Achsen der Koordinatensysteme ![]() und
und ![]() befindet. Dann
wird eine Translation durchgeführt mit dem Wert der Ursprungsposition
von
befindet. Dann
wird eine Translation durchgeführt mit dem Wert der Ursprungsposition
von ![]() . Cosinus und Sinus des Drehwinkels
. Cosinus und Sinus des Drehwinkels ![]() ergeben sich
gerade aus den Werten
ergeben sich
gerade aus den Werten ![]() bzw.
bzw. ![]() , wobei die
Einheitsvektoren
, wobei die
Einheitsvektoren ![]() und
und ![]() die Basis für Koordinatensystem
die Basis für Koordinatensystem ![]() darstellen.
darstellen.
Also läßt sich in obigem Beispiel der Punkt ![]() wie folgt transformieren:
wie folgt transformieren:
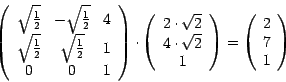
Um einen Punkt
![]() im Koordinatensystem
im Koordinatensystem ![]() bzgl. des Koordinatensystems
bzgl. des Koordinatensystems ![]() zu spezifizieren, verwendet man die inverse
Matrix zu
zu spezifizieren, verwendet man die inverse
Matrix zu
![]() :
: