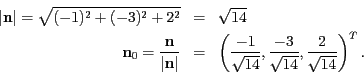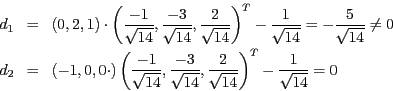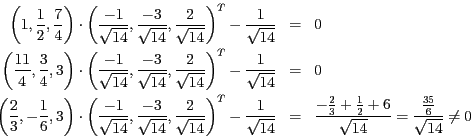Aufgabe 1.1 (30 Punkte)
Sei das Dreieck
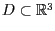 defniert durch die Eckpunkte
defniert durch die Eckpunkte
- Geben Sie die Ebene
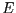 , die das Dreieck enthält mittels Hessescher
Normalenform und Parameterdarstellung an.
, die das Dreieck enthält mittels Hessescher
Normalenform und Parameterdarstellung an.
- Bestimmen Sie jeweils die Abstände
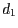 , bzw.
, bzw. 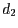 der Punkte
der Punkte
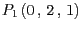 , bzw.
, bzw.
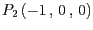 zu der Ebene
zu der Ebene 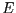 . Wählen Sie zur Berechnung eine der in (a) ermittelten
Darstellungen und erläutern Sie ihre Wahl.
. Wählen Sie zur Berechnung eine der in (a) ermittelten
Darstellungen und erläutern Sie ihre Wahl.
- Entscheiden Sie für die drei Punkte
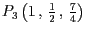 ,
,
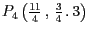 und
und
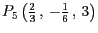 jeweils, ob sie sich auf der Ebene
jeweils, ob sie sich auf der Ebene 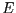 befinden.
befinden.
Musterlösung vom 02.05.2012:
- Man berechnet zunächst die (nichtnormalisierte) Normale
und erhält durch Normieren die Normale
Der Abstand 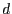 zum Ursprung ist also
zum Ursprung ist also
Und die HNF somit
Die Parameterdarstellung hat allgemein die Form
Wir wählen 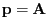 und die Richtungsvektoren ergeben sich
aus
und die Richtungsvektoren ergeben sich
aus
Also lautet die Parameterdarstellung
- Wir wählen die HNF zur Berechnung des Abstandes, da sich dieser durch
Einsetzen der Punkte unmittelbar ergibt.
Der Punkt 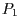 liegt also nicht in der Ebene, aber Punkt
liegt also nicht in der Ebene, aber Punkt 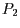 .
.
- Wir setzen wieder in die HNF ein und testen, ob das Ergebnis 0 ist.
Die Punkte 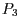 und
und 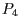 befinden sich also auf der Ebene
und
befinden sich also auf der Ebene
und 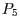 nicht.
nicht.



![]() defniert durch die Eckpunkte
defniert durch die Eckpunkte