


Aufgabe 1.2 (30 Punkte)
Seien die Punkte
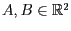 durch
durch
gegeben.
- Geben Sie die Gerade
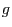 , die durch
, die durch 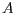 und
und 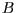 geht mittels impliziter
Darstellung, Parameterdarstellung und Hessescher Normalenform an und
zeichnen Sie sie.
geht mittels impliziter
Darstellung, Parameterdarstellung und Hessescher Normalenform an und
zeichnen Sie sie.
- Konstruieren Sie eine Gerade
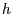 , die die Gerade
, die die Gerade 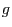 im Punkt
im Punkt
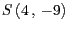 in einem Winkel von
in einem Winkel von
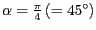 schneidet und erweitern Sie ihre Zeichnung aus (a). Geben Sie die
Gerade
schneidet und erweitern Sie ihre Zeichnung aus (a). Geben Sie die
Gerade 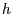 mittels der Parameterdarstellung an.
mittels der Parameterdarstellung an.
- Gegeben sei nun zusätzlich der Punkt
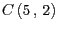 . Entscheiden
Sie jeweils rechnerisch für die Punkte
. Entscheiden
Sie jeweils rechnerisch für die Punkte
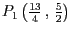 und
und
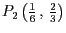 ob diese sich
innerhalb des von
ob diese sich
innerhalb des von 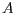 ,
, 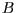 und
und 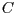 definierten Dreiecks befinden.
definierten Dreiecks befinden.
Musterlösung vom 02.05.2012:
- Für die HNF berechnen wir zunächst den Richtungsvektor
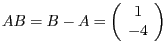 der Geraden und erhalten für die nicht normierte Normale
der Geraden und erhalten für die nicht normierte Normale
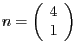 . Schließlich erhalten wir nach dem Normieren die gesuchte Normale
. Schließlich erhalten wir nach dem Normieren die gesuchte Normale
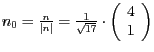 . Für den Abstand
. Für den Abstand 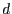 setzen wir den Punkt
setzen wir den Punkt 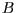 in die HNF ein und
erhalten
in die HNF ein und
erhalten
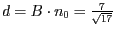 . Damit erhalten wir
die HNF
. Damit erhalten wir
die HNF
Eine implizite Darstellung erhält man durch das Setzen von
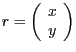 , anschließendes Ausmultiplizieren und Multiplikation mit
, anschließendes Ausmultiplizieren und Multiplikation mit 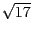 .
.
Die Parameterdarstellung lautet einfach
- Gesucht ist eine Gerade
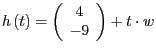 , die die Gerade
, die die Gerade
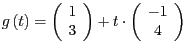 in einem Winkel von
in einem Winkel von
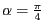 schneidet. Dies ist genau
dann der Fall, wenn der Richtingsvektor
schneidet. Dies ist genau
dann der Fall, wenn der Richtingsvektor 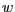 von
von
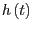 mit dem Richtungsvektor
mit dem Richtungsvektor
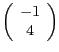 einen Winkel von
einen Winkel von 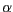 einschließt. Eine Formel für den Winkel
einschließt. Eine Formel für den Winkel
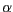 zwischen zwei Vektoren
zwischen zwei Vektoren 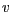 und
und 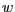 lautet z.B.
lautet z.B.
Wir setzen nun ein und erhalten
Es sei angemerkt, dass der Vektor 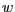 nicht eindeutig definiert ist.
Erfüllt nämlich ein Vektor
nicht eindeutig definiert ist.
Erfüllt nämlich ein Vektor 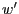 die Bedingung, so natürlich
auch jeder Vektor
die Bedingung, so natürlich
auch jeder Vektor
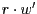 mit
mit 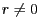 . Wir setzen also
die Koordinate
. Wir setzen also
die Koordinate 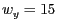 und erhalten
und erhalten
Wir erhalten also die beiden Lösungen
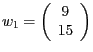 und
und
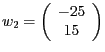 , die zwei verschiedene Geraden
, die zwei verschiedene Geraden
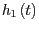 und
und
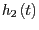 repräsentieren, die die Gerade
repräsentieren, die die Gerade
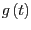 im Winkel von
im Winkel von
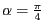 schneiden. Es ergeben sich also die beiden Lösungen
schneiden. Es ergeben sich also die beiden Lösungen
Alternative: Da wir hier den Winkel
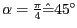 gegeben haben, lässt sich die zu konstruierende Gerade
gegeben haben, lässt sich die zu konstruierende Gerade 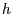 als Winkelhalbierende
zwischen dem Richtungsvektor
als Winkelhalbierende
zwischen dem Richtungsvektor 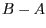 von
von 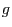 und der Normale
und der Normale 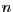 von
von 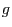 interpretieren. Diese erhält man durch Addition der beiden
Vektoren, also
interpretieren. Diese erhält man durch Addition der beiden
Vektoren, also
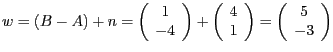 . Vorsicht: Hierzu müssen beide Vektoren die gleiche Länge
haben.
. Vorsicht: Hierzu müssen beide Vektoren die gleiche Länge
haben.
- Um zu bestimmen, ob ein Punkt innerhalb eines Dreiecks ist, hat man
mehrere Möglichkeiten.
Möglichkeit 1 (Algorithmus: Punkt in konvexem Polygon). Wir
stellen zunächst die impliziten Darstellungen der drei Geraden auf,
die durch die Seiten des Dreiecks definiert werden. Anhand von der
Kante 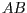 wird dies explizit durchgeführt. Zunächst berechnen wir
den Richtungsvektor
wird dies explizit durchgeführt. Zunächst berechnen wir
den Richtungsvektor
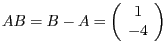 . Wir erhalten die Normale durch Vertauschen der Einträge und Negieren
des oberen Eintrages, also
. Wir erhalten die Normale durch Vertauschen der Einträge und Negieren
des oberen Eintrages, also
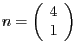 . Dadurch lautet eine implizite Darstellung
. Dadurch lautet eine implizite Darstellung
Wir berechnen 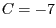 durch Einsetzen des Punktes
durch Einsetzen des Punktes
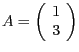 , erhalten also insgesamt
, erhalten also insgesamt
Analog berechnen wir
Jetzt setzen wir den Punkt 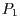 in die drei Gleichungen ein.
in die drei Gleichungen ein.
Da wir zwei unterschiedliche Vorzeichen haben, liegt 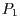 außerhalb
des Dreiecks. Einsetzen von
außerhalb
des Dreiecks. Einsetzen von 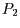 liefert
liefert
Auch hier erhalten wir zwei unterschiedliche Vorzeichen, womit auch
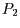 nicht im Dreieck liegt.
nicht im Dreieck liegt.
Möglichkeit 2 (Baryzentrische Koordinaten). Wir stellen die
Formel für die baryzentrischen Koordinaten mit 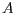 als Stützvektor,
sowie
als Stützvektor,
sowie 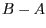 und
und 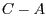 als Richtungsvektoren. Damit erhalten wir
als Richtungsvektoren. Damit erhalten wir
Wir berechnen für 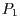 die Parameter
die Parameter 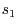 und
und 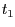 , sodass
, sodass
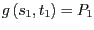 mittels einem linearen Gleichungssystems.
Wenn die Parameter den Bedingungen
mittels einem linearen Gleichungssystems.
Wenn die Parameter den Bedingungen
genügen, liegt der Punkt im Dreieck. Wir erhalten also das LGS
Da
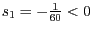 liegt
liegt 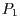 nicht in dem Dreieck. Für
nicht in dem Dreieck. Für
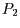 erhalten wir das LGS
erhalten wir das LGS
Da
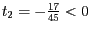 liegt
liegt 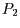 nicht in dem Dreieck.
nicht in dem Dreieck.



![]() durch
durch
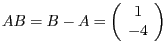 der Geraden und erhalten für die nicht normierte Normale
der Geraden und erhalten für die nicht normierte Normale
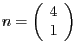 . Schließlich erhalten wir nach dem Normieren die gesuchte Normale
. Schließlich erhalten wir nach dem Normieren die gesuchte Normale
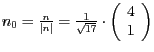 . Für den Abstand
. Für den Abstand  , anschließendes Ausmultiplizieren und Multiplikation mit
, anschließendes Ausmultiplizieren und Multiplikation mit 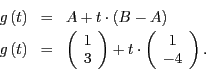
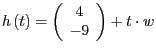 , die die Gerade
, die die Gerade
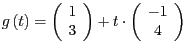 in einem Winkel von
in einem Winkel von
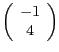 einen Winkel von
einen Winkel von 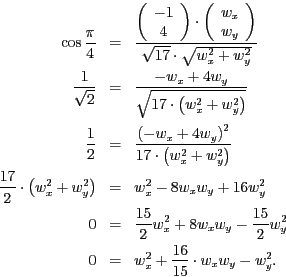
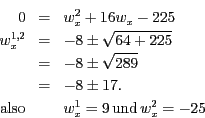
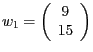 und
und
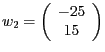 , die zwei verschiedene Geraden
, die zwei verschiedene Geraden
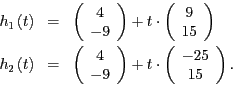
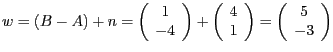 . Vorsicht: Hierzu müssen beide Vektoren die gleiche Länge
haben.
. Vorsicht: Hierzu müssen beide Vektoren die gleiche Länge
haben.
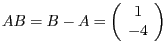 . Wir erhalten die Normale durch Vertauschen der Einträge und Negieren
des oberen Eintrages, also
. Wir erhalten die Normale durch Vertauschen der Einträge und Negieren
des oberen Eintrages, also
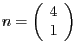 . Dadurch lautet eine implizite Darstellung
. Dadurch lautet eine implizite Darstellung
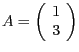 , erhalten also insgesamt
, erhalten also insgesamt
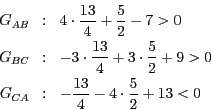
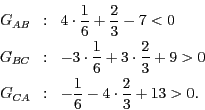
![\begin{eqnarray*}
\left(i\right) & & s_{1}\in\left[0,1\right]\\
\left(ii\right)...
...,1\right]\\
\left(iii\right) & & s_{1}+t_{1}\in\left[0,1\right]
\end{eqnarray*}](img86.gif)