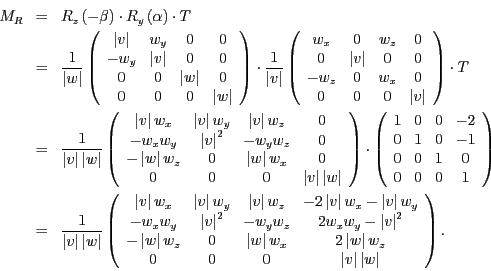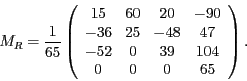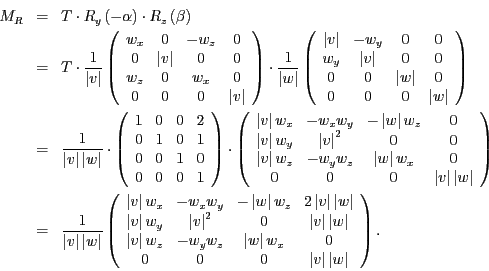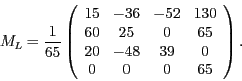Aufgabe 3.1 (40 Punkte)
Seien die Punkte
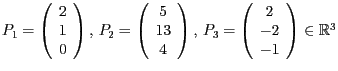 gegeben. Konstruieren Sie eine Matrix
gegeben. Konstruieren Sie eine Matrix 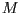 , die den Punkt
, die den Punkt 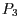 um die von
um die von 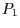 und
und 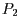 definierte Gerade um den Winkel
definierte Gerade um den Winkel
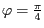 dreht. Gehen Sie dabei folgendermaßen vor:
dreht. Gehen Sie dabei folgendermaßen vor:
- Geben Sie die Gerade
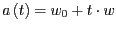 , die durch
, die durch
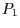 und
und 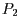 geht, in Parameterform an, sodass
geht, in Parameterform an, sodass
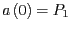 und
und
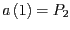 .
.
- Konstruieren Sie die Translationsmatrix
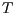 , sodass der Nullpunkt
auf der Geraden
, sodass der Nullpunkt
auf der Geraden
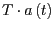 liegt.
liegt.
- Konstruieren Sie die Rotationsmatrix
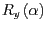 um
die
um
die 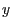 -Achse und mit dem Winkel
-Achse und mit dem Winkel 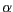 , sodass die Gerade
, sodass die Gerade
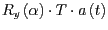 in der
in der 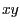 -Ebene liegt.
-Ebene liegt.
- Konstruieren Sie die Rotationsmatrix
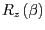 um
die
um
die 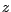 -Achse und mit dem Winkel
-Achse und mit dem Winkel 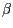 , sodass die Gerade
, sodass die Gerade
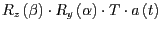 auf der
auf der 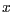 -Achse liegt.
-Achse liegt.
- Konstruieren Sie die Rotationsmatrix
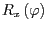 ,
die einen Punkt
,
die einen Punkt 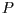 um die
um die 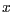 -Achse dreht.
-Achse dreht.
- Konstruieren Sie die Transformationen
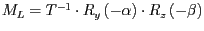 und
und
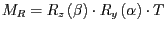 exakt.
exakt.
- Berechnen Sie den Punkt
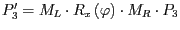 mittels der Klasse Matrix4f. Erzeugen Sie dazu drei Matrizen,
in die Sie die Werte von
mittels der Klasse Matrix4f. Erzeugen Sie dazu drei Matrizen,
in die Sie die Werte von 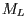 ,
, 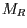 und
und
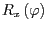 explizit eintragen und berechnen Sie das Produkt mittels der Methode
Matrix4f.mul(...) und speichern Sie die Ergebnismatrix in
einer neuen Variable. Erzeugen Sie anschließend einen Vector4f
mit den Werten des Punktes
explizit eintragen und berechnen Sie das Produkt mittels der Methode
Matrix4f.mul(...) und speichern Sie die Ergebnismatrix in
einer neuen Variable. Erzeugen Sie anschließend einen Vector4f
mit den Werten des Punktes 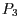 und transformieren Sie diesen
mittels der Methode Matrix4f.transform(...). Lassen Sie sich
das Ergebnis auf der Konsole ausgeben.
und transformieren Sie diesen
mittels der Methode Matrix4f.transform(...). Lassen Sie sich
das Ergebnis auf der Konsole ausgeben.
Hinweis: Alle Berechnungen in den Schritten 1. bis 6. haben
exakt zu sein. Sie müssen ihrem Tutor jeden Schritt klarmachen
(am Besten mithilfe einer oder mehrerer Skizzen). Es wird empfohlen,
die Matrizen
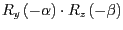 und
und
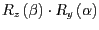 zumächst
allgemein aufzustellen und zusammenzurechnen, bevor Sie die Werte
explizit einsetzen. Die Winkel
zumächst
allgemein aufzustellen und zusammenzurechnen, bevor Sie die Werte
explizit einsetzen. Die Winkel 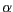 und
und 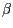 müssen zu keinem
Zeitpunkt exakt aufgestellt werden.
müssen zu keinem
Zeitpunkt exakt aufgestellt werden.
Musterlösung vom 16.05.2012:
[scale=0.25]rotation
- Die Geradengleichung ist
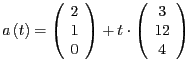 . Damit ist
. Damit ist
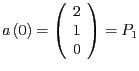 und
und
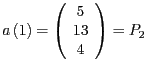 . Dann ist
. Dann ist
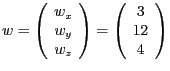 und die Projektion
und die Projektion 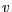 von
von 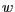 auf die
auf die 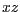 -Ebene ist
-Ebene ist
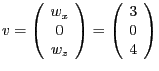 .
.
- Wir konstruieren eine Translationsmatrix
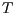 , sodass
, sodass
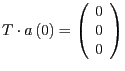 . Wir translatieren also um
. Wir translatieren also um
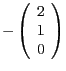 . Damit ist
. Damit ist
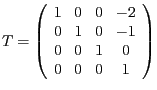 .
.
- Wir rotieren um die
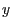 -Achse mit dem Winkel
-Achse mit dem Winkel 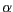 . Aus der Zeichnung
erhalten wir die Zusammenhänge
. Aus der Zeichnung
erhalten wir die Zusammenhänge
Also lautet die Rotationsmatrix
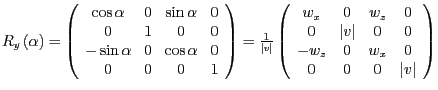 .
.
- Wir rotieren um die
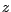 -Achse mit dem Winkel
-Achse mit dem Winkel
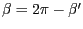 (da wir mit dem Uhrzeigersinn drehen müssen). Aus der Zeichnung erhalten
wir die Zusammenhänge
(da wir mit dem Uhrzeigersinn drehen müssen). Aus der Zeichnung erhalten
wir die Zusammenhänge
Also lautet die Rotationsmatrix
- Wir rotieren um die
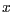 -Achse mit dem Winkel
-Achse mit dem Winkel
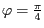 .
Wir setzen
.
Wir setzen
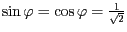 direkt in
die Matrix ein und erhalten
direkt in
die Matrix ein und erhalten
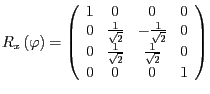 .
.
- Wir konstruieren
Einsetzen von
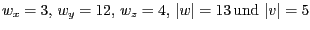 liefert
liefert
Für die Inverse Matrix erhalten wir
Einsetzen liefert
- /home/cg/2012/Uebung/Blatt3/Lsg/CG12Blatt3.zip



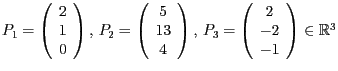 gegeben. Konstruieren Sie eine Matrix
gegeben. Konstruieren Sie eine Matrix 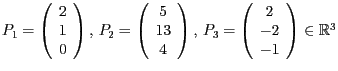 gegeben. Konstruieren Sie eine Matrix
gegeben. Konstruieren Sie eine Matrix ![]() , die den Punkt
, die den Punkt ![]() um die von
um die von ![]() und
und ![]() definierte Gerade um den Winkel
definierte Gerade um den Winkel
![]() dreht. Gehen Sie dabei folgendermaßen vor:
dreht. Gehen Sie dabei folgendermaßen vor:
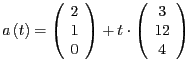 . Damit ist
. Damit ist
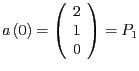 und
und
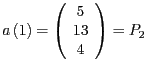 . Dann ist
. Dann ist
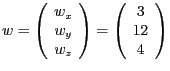 und die Projektion
und die Projektion 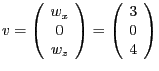 .
.
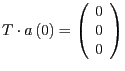 . Wir translatieren also um
. Wir translatieren also um
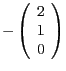 . Damit ist
. Damit ist
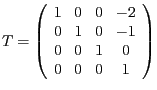 .
.
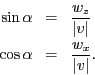
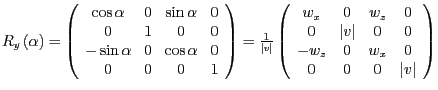 .
.
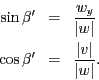
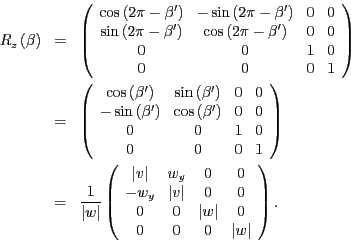
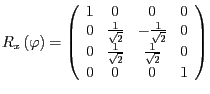 .
.