


Aufgabe 3.2 (25 Punkte)
Seien wieder die Punkte
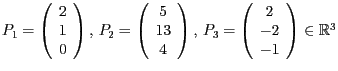 gegeben. Konstruieren Sie wieder eine Matrix
gegeben. Konstruieren Sie wieder eine Matrix 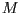 , die den Punkt
, die den Punkt
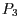 um die von
um die von 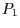 und
und 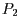 definierte Gerade um den
Winkel
definierte Gerade um den
Winkel
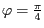 dreht. Gehen Sie diesmal folgendermaßen
vor:
dreht. Gehen Sie diesmal folgendermaßen
vor:
- Geben Sie die Gerade
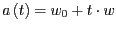 , die durch
, die durch
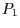 und
und 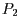 geht, in Parameterform an, sodass
geht, in Parameterform an, sodass
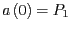 und
und
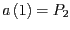 .
.
- Konstruieren Sie einen Vektor
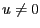 , sodass
, sodass 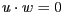 , d.h.
, d.h.
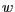 steht orthogonal auf
steht orthogonal auf 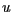 und den Vektor
und den Vektor 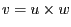 .
.
- Konstruieren Sie die Basentransformationsmatrix
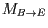 ,
die einen Punkt
,
die einen Punkt 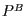 , beschrieben in dem Koordinatensystem
, beschrieben in dem Koordinatensystem
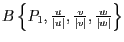 ,
in einen Punkt
,
in einen Punkt 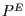 , beschrieben in dem Standardkoordinatensystem
, beschrieben in dem Standardkoordinatensystem
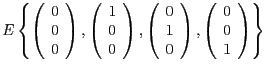 , überführt.
, überführt.
- Konstruieren Sie die Rotationsmatrix
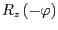 ,
die einen Punkt
,
die einen Punkt 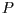 um die
um die 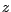 -Achse mit dem Winkel
-Achse mit dem Winkel
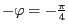 dreht.
dreht.
- Berechnen Sie
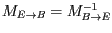 mit der
von Matrix4f bereitgestellten Methode und führen Sie Punkt
7. der vorherigen Aufgabe mit den folgenden Matrizen durch:
mit der
von Matrix4f bereitgestellten Methode und führen Sie Punkt
7. der vorherigen Aufgabe mit den folgenden Matrizen durch:
-
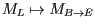
-
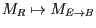
-
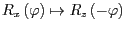
- Warum erhalten Sie (sofern Sie keinen Fehler gemacht haben) dasselbe
Ergebnis wie in Aufgabe 1?
Hinweis: Alle Berechnungen in den Schritten 1. bis 4. haben
exakt zu sein.
Musterlösung vom 16.05.2012:
- s. Aufgabe 1.1
- Sei
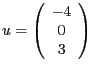 . Damit gilt
. Damit gilt
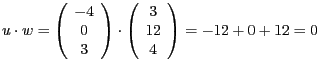 und
und
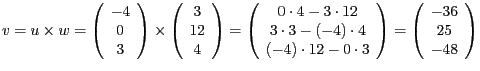 .
.
- Die Transformationsmatrix erhalten wir, indem wir die Basisvektoren
als Spalten der Matrix schreiben und in die vierte Spalte den Urpsrung
des Koordinatensystem, also
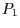 . Wir erhalten
. Wir erhalten
Exkurs Lineare Algebra: Eine solche Matrix ist besonders
leicht zu invertieren, da sie die Gestalt
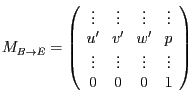 hat, wobei die Vektoren
hat, wobei die Vektoren
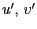 und
und 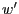 eine Orthonormalbasis sind und
eine Orthonormalbasis sind und 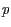 ein beliebiger Punkt. Die Inverse
ist dann
ein beliebiger Punkt. Die Inverse
ist dann
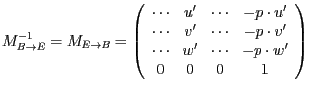 . In unserem Fall ist also
. In unserem Fall ist also
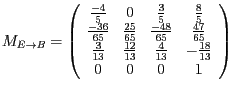 .
.
- Für die Rotationsmatrix erhalten wir einfach
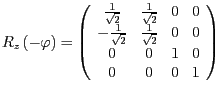 .
.
- /home/cg/2012/Uebung/Blatt3/Lsg/CG12Blatt3.zip
- Die Transformation
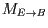 sorgt dafür, dass alle Punkte
bezüglich des Koordinatensystems beschrieben werden, dessen
sorgt dafür, dass alle Punkte
bezüglich des Koordinatensystems beschrieben werden, dessen 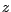 -Achse
genau der Gerade entspricht. Daher führt eine Rotation des Punktes
um die
-Achse
genau der Gerade entspricht. Daher führt eine Rotation des Punktes
um die 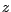 -Achse und anschließendes Zurücktransformieren mittels
-Achse und anschließendes Zurücktransformieren mittels
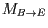 zu der gleichen Operation.
zu der gleichen Operation.



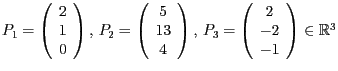 gegeben. Konstruieren Sie wieder eine Matrix
gegeben. Konstruieren Sie wieder eine Matrix 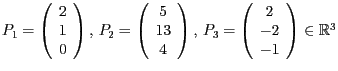 gegeben. Konstruieren Sie wieder eine Matrix
gegeben. Konstruieren Sie wieder eine Matrix ![]() , die den Punkt
, die den Punkt
![]() um die von
um die von ![]() und
und ![]() definierte Gerade um den
Winkel
definierte Gerade um den
Winkel
![]() dreht. Gehen Sie diesmal folgendermaßen
vor:
dreht. Gehen Sie diesmal folgendermaßen
vor:
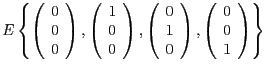 , überführt.
, überführt.
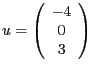 . Damit gilt
. Damit gilt
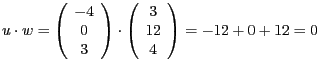 und
und
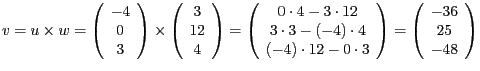 .
.

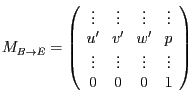 hat, wobei die Vektoren
hat, wobei die Vektoren
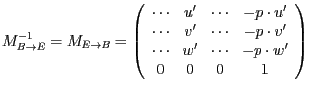 . In unserem Fall ist also
. In unserem Fall ist also
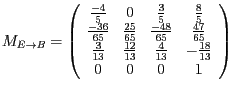 .
.
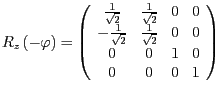 .
.