Aufgabe 7.4 (20 Punkte)

Gegeben seien folgender VertexBuffer VB und IndexBuffer IB

$$\begin{eqnarray*} VB & = & \left\{ -2,-1,0,2,-2.5,0,0,1,0\right\} \\ IB & = & \left\{ 0,2,1\right\} . \end{eqnarray*}$$

Das Vertexlayout ist definiert durch: $\left\{ p_{x},p_{y},p_{z}\right\}$. Diese Daten sollen nun mit dem Primitiven Typen GL_TRIANGLE in OpenGL gerendert werden. Rendern geschieht in OpenGL mit Hilfe der Graphics Pipeline. Der gesamte Renderprozess lässt sich in weitere Prozesse (sogenannte Stages) zerlegen:

1. Vertex Shader
2. Primitive Assembly
3. Primitive Processing
4. Rasterizer
5. Fragment Shader
6. Per Fragment Operations

In dieser Aufgabe sollen Sie die oben gegebenen Daten manuell durch die Stages Vertex Shader, Primitive Assembly und Primitive Processing führen. Halten Sie dabei die Aufgaben jeder einzelnen Stage schriftlich fest und führen Sie alle relevanten Operationen schriftlich durch. Geben Sie den Output jeder Stage in Abhängigkeit der Eingangsdaten an. Führen Sie bei Ihren Berechnungen Brüche möglichst lange mit und runden Sie endgültige Ergebnisse auf drei Stellen nach dem Komma. Zeichnen Sie das Ergebnis nach dem Primitive Processing ohrtogonal projiziert in die $XY$ - Ebene ($x,y\in[-1,1]$) qualitativ und machen Sie neu erzeugte Vertices und Primitive erkenntlich. Benutzen Sie für die View- und Projektionsmatrix folgende Parameter.

• Kameraposition: $\left(1,0,-2\right)$
• Blickrichtung: $\left(0,0,1\right)$
• Projektionsparameter: $l=b=-0.01;\, r=t=n=0.01;\, f=100$
• Zum Vergleich Viewmatrix und Projektionsmatrix

$$\begin{eqnarray*} V & = & \left(\begin{array}{cccc} -1 & 0 & 0 & 1\\ 0 & 1 & 0 ... ...\\ 0 & 0 & -1.002 & -0.02\\ 0 & 0 & -1 & 0 \end{array}\right). \end{eqnarray*}$$

Verwenden Sie für die programmierbaren Stages der Pipeline folgende Shader.

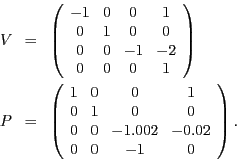
Vertexshader

#version 150 core

uniform mat4 viewProj;

in vec3 vs_in_pos;

void main(void) {

 gl_Position = viewProj * vec4(vs_in_pos,1);

 fs_in_red = vs_in_red;

}

Fragmentshader

#version 150 core

out vec4 fs_out_color;

void main(void) {

 fs_out_color = vec4(1);

}

Gegeben sei nun folgender VertexBuffer $VB$ und IndexBuffer $IB$.

$$\begin{eqnarray*} VB & = & \left\{ -2,\,-1,\,0,\,2,\,-2.5,\,0,\,0,\,1,\,0\right\} \\ IB & = & \left\{ 0,\,1,\,2\right\} . \end{eqnarray*}$$

Führen Sie mit diesen Daten ebenfalls die Graphics Pipeline aus. Gleichbleibende Berechnungen können Sie aus dem ersten Aufgabenteil übernehmen.

Musterlösung vom 13.06.2012:

Vertex Shader

Programmierbarer Teil der Pipeline. Vertexdaten werden transformiert.

Da jeweils drei Werte des Floatbuffers einen Vertex ergeben, werden drei Shaderinstanzen für die Vertices $v0=\{-2,\,-1,\,0\}$ $v1=\{2,\,-2.5,\,0\}$ $v2=\{0,\,1,\,0\}$erzeugt.

Nach Anwendung der View - und Projektionsmatrix liegen die Daten in den Clipping Coordinates.

Output: Koordinaten in Clipping Coordinates $v0^{cc}=\{3,\,-1,\,1.984,\,2\}$ $\, v1^{cc}=\{-1,\,-2.5,\,1.984,\,2\}$ $\, v2^{cc}=\{1,\,1,\,1.984,\,2\}$

Primitive Assembly

Fester Teil der Pipeline. Die Koordinaten werden über die angegebene Topologie (GL_TRIANGLE) zu einem Dreieck.

Ouput: Ein einziges Primitiv (Dreieck). ( $v0^{cc}=\{3,\,-1,\,1.984,\,2\}$ $v1^{cc}=\{-1,\,-2.5,\,1.984,\,2\}$ $v2^{cc}=\{1,\,1,\,1.984,\,2\}$)

Primitive Processing

Fester Teil der Pipeline. Hier werden die Primitive geclippt, die Koordinaten homogenisiert, auf das Anzeigedevice projiziert und schließlich gecullt.

Offenbar liegen $v0$ und $v1$ nicht innerhalb des kanonischen Viewvolume. Somit muss das Dreieck geclippt werden.

Schnittpunkte mit der Achse $x=2$:

Gerade von $v0$ nach $v2$

$v0+t\cdot(v2-v0)=(3,\,-1)+t\cdot(2,\,-2)$

$(3,\,-1)+t*(2,\,-2)=(2,\, y)\rightarrow y=0$

Gerade von $v0$ nach $v1$

$v0+t\cdot(v1-v0)=(3,\,-1)+t\cdot(-4,\,-1.5)$

$(3,\,-1)+t\cdot(-4,\,-1.5)=(2,\, y)\rightarrow y=-1,375$

Schnittpunkt mit der Achse $y=-2$:

Gerade von $v2$ nach $v1$

$v1+t\cdot(v2-v1)=(-1,\,-2.5)+t\cdot(2,\,3.5)$

$(-1,\,-2.5)+t\cdot(2,\,3.5)=(x,\,-2)\rightarrow x=-0.714$

Gerade von $v0$ nach $v1$

$v0+t\cdot(v1-v0)=(3,\,-1)+t\cdot(-4,\,-1.5)$

$(3,\,-1)+t\cdot(-4,\,-1.5)=(x,\,-2)\rightarrow x=1/3$

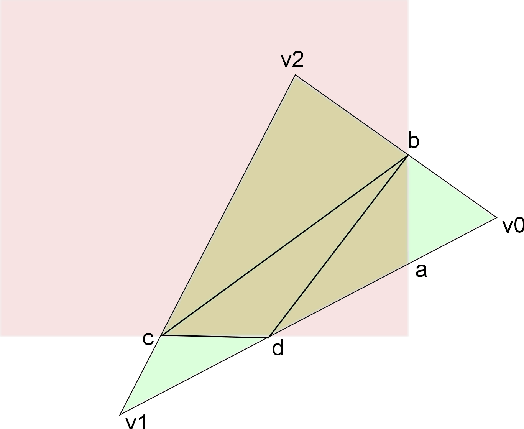
Somit ergeben sich vier neue Koordinaten, die wieder zu Dreiecken $di$ zusammengesetzt werden müssen.

Ergebnis

$d0=(c,\, b,\, v2)$, $d1=(c,\, d,\, b)$, $d2=(d,\, a,\, b)$

$c=(-0.714,\,-2)$, $d=(1/3,\,-2)$, $a=(2,\,-1,375)$, $b=(2,\,0)$

Im nächsten Schritt werden die Koordinaten homogenisiert.

Homogenisieren ergibt:

$v2^{h}=\{0.5,\,0.5,\,0.992,\,1\}$

$vc^{h}=\{-0.714/1.984,\,-2/1.984,\,0.992,\,1\}$

$vd^{h}=\{1/(3*1.984),\,-2/1.984,\,0.992,\,1\}$

$va^{h}=\{2/1.984,\,-1,375/1.984,\,0.992,\,1\}$

$vb^{h}=\{2/1.984,\,0,\,0.992,\,1\}$

Hiernach werden die Koordinaten auf den Viewport projiziert:

Hier beispielhaft für die Koordinate $v2^{h}$

$(1+v2^{h}.x)\cdot(width-1)/2=v2^{w}.x$

$(1+v2^{h}.y)\cdot(height-1)/2=v2^{w}.y$

$v2^{h}.z=v2^{w}.z$

Im letzten Schritt werden die Dreiecke gecullt. Da der positive Drehsinn Counter Clockwise gewählt ist und die Koordinaten in der Reihenfolge $0,2,1$ gerendert werden, bestehen die Dreiecke den Test (vergl. Bild).

Output: Drei Dreiecke $d0$, $d1$und $d2$.

Zweiter Teil: Dreieck wird gecullt. Alle notwendigen Berechnungen lassen sich von oben übernehmen.