Zweite Normalform

Ein Attribut heißt Primärattribut , wenn es in mindestens einem Schlüsselkandidaten vorkommt, andernfalls heißt es Nichtprimärattribut.

Ein Relationenschema $\cal$R ist in zweiter Normalform falls gilt:

• $\cal$R ist in der ersten Normalform
• Jedes Nichtprimär-Attribut A $\in$ $\cal$R ist voll funktional abhängig von jedem Schlüsselkandidaten.

Seien also $\kappa_{1}^{}$,...,$\kappa_{n}^{}$ die Schlüsselkandidaten in einer Menge F von FDs. Sei A  $\in$ $\cal$R - ($\kappa_{1}^{}$ $\cup$ ... $\cup$ $\kappa_{n}^{}$) ein Nichtprimärattribut . Dann muß für 1 $\leq$ j $\leq$ n gelten:

$$\kappa_{j}^{}$$ $$\dot{\rightarrow}$$ A  $$\in$$  F ⁺

Folgende Tabelle verletzt offenbar diese Bedingung:

MatrNr VorlNr Name Semester

26120 5001 Fichte 10

27550 5001 Schopenhauer 6

27550 4052 Schopenhauer 6

28106 5041 Carnap 3

28106 5052 Carnap 3

28106 5216 Carnap 3

28106 5259 Carnap 3

... ... ... ...

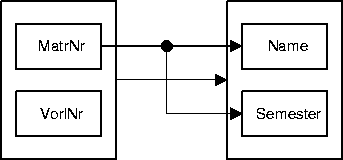
Abbildung 10.1 zeigt die funktionalen Abhängigkeiten der Relation StudentenBelegung. Offenbar ist diese Relation nicht in der zweiten Normalform, denn Name ist nicht voll funktional abhängig vom Schlüsselkandidaten {MatrNr, VorlNr}, weil der Name alleine von der Matrikelnummer abhängt.

Graphische Darstellung der funktionalen Abhängigkeiten von StudentenBelegung

Als weiteres Beispiel betrachten wir die Relation

Hörsaal : { [Vorlesung, Dozent, Termin, Raum] }

Eine mögliche Ausprägung könnte sein:

Vorlesung Dozent Termin Raum

Backen ohne Fett Kant Mo, 10:15 32/102

Selber Atmen Sokrates Mo, 14:15 31/449

Selber Atmen Sokrates Di, 14:15 31/449

Schneller Beten Sokrates Fr, 10:15 31/449

Die Schlüsselkandidaten lauten:

• {Vorlesung, Termin}
• {Dozent, Termin}
• {Raum, Termin}

Alle Attribute kommen in mindestens einem Schlüsselkandidaten vor. Also gibt es keine Nichtprimärattribute, also ist die Relation in zweiter Normalform.