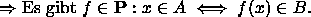
( P = Menge aller in Polynomzeit berechenbaren Funktionen)
NP : = {L : Zu gegebener Instanz x und Beweisvorschlag y kann in
Polynomzeit überprüft werden, ob y beweist: x ![]() L}
( L = Ja-Nein-Problem)
L}
( L = Ja-Nein-Problem)
L0 ist NP -vollständig, wenn
Nachweis der NP -Vollständigkeit, über ein ``erstes''
NP -vollständigiges Problem L1 , für ein ``neues''
NP -vollständiges Problem L2 durch Finden einer Reduktion
L1![]() L2 . (``Erstes'' NP -vollständigiges Problem L1
fand Cook 1972: Satisfiability Problem) Beispiele für Reduktion:
L2 . (``Erstes'' NP -vollständigiges Problem L1
fand Cook 1972: Satisfiability Problem) Beispiele für Reduktion:
Beispiele für Reduktion:
| 1.) | Independent Set | |
Vertexcover |
| (siehe Abschnitt Independent Set) | |||
| 2.) | 3-Färbbarkeit | |
Independent Set |
| Als Ja-Nein-Problem | Gibt es eine | |
Gibt es ein Independent Set mit |
| formulieren: | 3-Färbung? | bestimmter Anzahl von Knoten? |
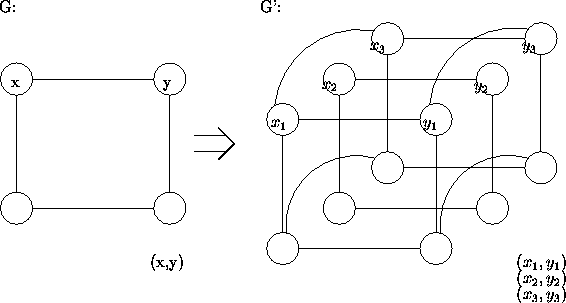
| |
Aus jeder ``Dreier''-Gruppe gehört genau ein Knoten zum
Independent Set I . Falls i -ter Knoten |
|
|
Füge jeweils i -ten Knoten aus jeder ``Dreier''-Gruppe zu I hinzu, wobei i die Farbe des entsprechenden Knotens in G ist. |
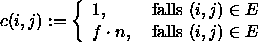
Sei A der Näherungsalgorithmus mit Schranke f . Wende A auf G' an.