Gilt für alle I :
![]()
![]() f
f ![]() Fehlerschranke
von A ist f ( f
Fehlerschranke
von A ist f ( f![]() 1 ).
1 ).
Näherungslösungen für TSP:
Bestimme Rundweg. Tausche Paare aus, falls
c(x,y) + c(a,b) > c(x,b) + c(a,y)
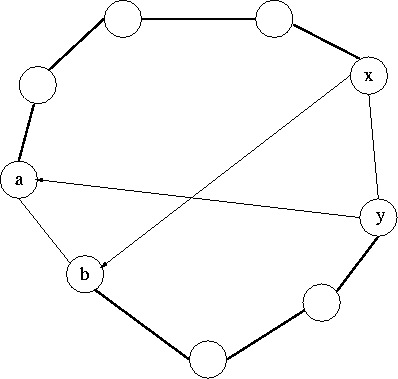
Keine konstante Fehlerschranke.
Im folgenden sei die Dreiecksungleichung erfüllt d.h.
c(x,z)![]() c(x,y) + c(y,z)
c(x,y) + c(y,z)![]() x,y,z
x,y,z ![]() V . (Insbesondere gilt also: G ist voll besetzt.)
V . (Insbesondere gilt also: G ist voll besetzt.)
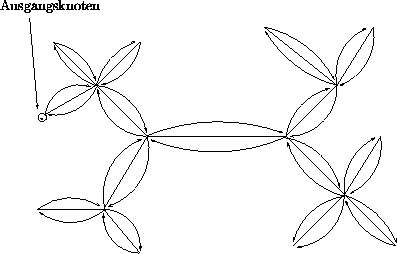
![]() Länge = 2c(MST) , da
c(MST) < c(TSP)
Länge = 2c(MST) , da
c(MST) < c(TSP) ![]() Umlauf
< 2c(TSP) .
Umlauf
< 2c(TSP) .
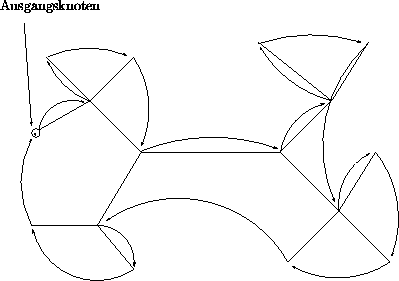
![]() Fehlerschranke f = 2 .
Fehlerschranke f = 2 .
(Wegen |V'| geradzahlig, ist das Matching perfekt.)
Alle Knoten haben geraden Grad (in G'' ). ![]() Graph G'' ist
eulersch (d.h. es ex. eine Eulertour in G'' ). Bestimme Eulertour K .
Es gilt:
c(K) = c(MST) + c(M) (
c(MST) < c(TSP),c(M) <
Graph G'' ist
eulersch (d.h. es ex. eine Eulertour in G'' ). Bestimme Eulertour K .
Es gilt:
c(K) = c(MST) + c(M) (
c(MST) < c(TSP),c(M) < ![]() · c(TSP) )
· c(TSP) )
Zur Begründung der weiter unten folgenden Vermutung benötigen wir den Begriff der NP-Vollständigkeit: