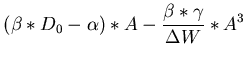Nächste Seite: Stabilität
Aufwärts: Proseminar Angewandte Systemwissenschaft SS
Vorherige Seite: Die induzierte Emission
Inhalt
Zusammenfassung der bisherigen Prozesse
Zunächst wollen wir uns einer elektromagnetischen Welle in einem
leeren Resonator zuwenden. Ihr zeitlicher Verlauf kann mit einer
Sinusschwingung beschrieben werden.
| |
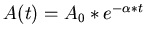 |
|
|
| |
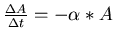 |
|
(5) |
Daraus folgt:
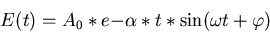 |
(6) |
Nun ist der Resonator aber mit Rubinatomen angefüllt, weshalb die
Amplitudenhöhe zeitlich auch von den vorgenannten Prozessen
abhängt. Durch die Absorbtion verliert sie abhängig von der
Anzahl an Atomen im Grundzustand, einem Proportionalitätsfaktor
 und von der Amplitude selbst Energie.
und von der Amplitude selbst Energie.
| |
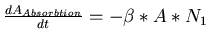 |
|
(7) |
| |
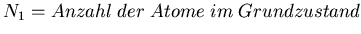 |
|
|
Durch die induzierte Emission gewinnt sie entsprechend:
| |
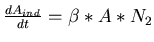 |
|
(8) |
| |
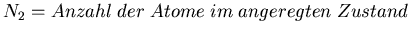 |
|
|
Somit ergibt sich ingesamt für die zeitliche Veränderung der
Amplitude:
,wobei
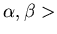 0 sind.
0 sind.
Diese Differentialgleichung
läßt sich mit einem exponentiellen Ansatz lösen.
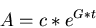 |
(10) |
Damit die Welle nicht (einfach) abklingt, muß G 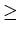 0 sein, was
auf die Gleichung
0 sein, was
auf die Gleichung
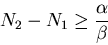 |
(11) |
führt. Dies ist die Laserbedingung von Schawlow und Townes.
Nun müssen wir uns aber mit dem Problem beschäftigen, daß nach
dem Boltzmannschen Verteilungsgesetz
bei Raumtemperatur das Verhältnis von angeregten zu Atomen im
Grundzustand
etwa 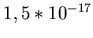 beträgt, G
also negativ ist. Um dieses zu ändern muß der Anteil, der sich im
angeregten Zustand befindlichen Atome durch Pumpen erhöht werden,
die Inversion
beträgt, G
also negativ ist. Um dieses zu ändern muß der Anteil, der sich im
angeregten Zustand befindlichen Atome durch Pumpen erhöht werden,
die Inversion
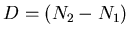 vergrößert werden.
vergrößert werden.
Der Faktor 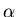 der Zerfallsrate im Resonator kann durch gute
Spiegelung verringert werden, allerdings soll immer noch Licht
nach außen dringen können 1 und im Faktor
der Zerfallsrate im Resonator kann durch gute
Spiegelung verringert werden, allerdings soll immer noch Licht
nach außen dringen können 1 und im Faktor  sind
spezifische Eigenschaften der verwendeten Atome enthalten. Aber
mit diesen beiden Faktoren wollen wir uns nicht weiter
beschäftigen. Wir betrachten sie im folgenden als fest gegeben
sind
spezifische Eigenschaften der verwendeten Atome enthalten. Aber
mit diesen beiden Faktoren wollen wir uns nicht weiter
beschäftigen. Wir betrachten sie im folgenden als fest gegeben
Nehmen wir nun an, daß wir die Laserbedingung
11 erfüllt hätten, dann wächst A exponentiell
an. Aufgrund des Energieerhaltungssatzes kann dieser Prozess aber
nicht unbeschränkt sein. ``Was ist also der begrenzende Faktor¿`
Das elektromagnetische Feld bezieht seine Energie aus den
Emissionen der in den Grundzustand zurückkehrenden Atome. Dies
bedeutet, daß D zeitlich nicht konstant sein kann. Ohne
Lasertätigkeit befindet sich D in einem durch Pumpen und
Abstrahlung schräg zur Resonatorebene und Wechselwirkungen der
Atome (auch die Randatome mit der Umgebung) untereinander
bestimmten Gleichgewichtszustand 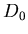 . Durch Lasertatigkeit
wird die tatsächliche Inversion D gegenüber
. Durch Lasertatigkeit
wird die tatsächliche Inversion D gegenüber 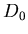 aufgrund der
Abgabe von Energie an das elektromagnetische Feld herabgesetzt. Um
diese Abnahme in die Amplitudengleichung einbauen zu können,
müssen wir einen Zusammenhang mit dieser finden. Die gespeicherte
Energie ist
aufgrund der
Abgabe von Energie an das elektromagnetische Feld herabgesetzt. Um
diese Abnahme in die Amplitudengleichung einbauen zu können,
müssen wir einen Zusammenhang mit dieser finden. Die gespeicherte
Energie ist
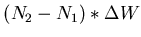 , also ist
, also ist
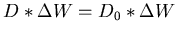 - abgegebende Energie an das EM-Feld.
- abgegebende Energie an das EM-Feld.
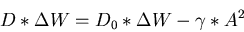 |
(13) |
Dies wird nun in die Gleichung 9 eingesetzt.
Nun enthält die Gleichung neben dem linearen Glied, welches für
sich alleine zu einem exponentiellen Anstieg führen würde, auch
eine bremsende Nichtlinearität. Betrachten wir nun als erstes
den stationären Fall:
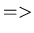
Durch die zweite Gleichung erhalten wir nur dann eine weitere
reelle Lösung, wenn
Dies ist genau die Laserbedingung 11. Noch eine
weitere Erkenntnis liefert uns die Gleichung 17. Die
Intensität des Laserlichtes nimmt bei verstärkten Pumpen linear
gegenüber 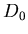 zu.
zu.




Nächste Seite: Stabilität
Aufwärts: Proseminar Angewandte Systemwissenschaft SS
Vorherige Seite: Die induzierte Emission
Inhalt
Thorsten Bojer
2000-05-16