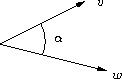
| Es gilt: |
|
|
|
|
|
|
||
|
|
|
Es gilt:
![]() beschreibt eine Ebene für
beschreibt eine Ebene für
![]() und Normalenvektor
und Normalenvektor ![]() . Alle Lösungsvektoren
. Alle Lösungsvektoren ![]() liegen
(als Punkte aufgefaßt) auf der Ebene. Das Skalarprodukt
aller Ebenenpunkte (als Vektoren geschrieben) mit dem
Normalenvektor ist konstant.
liegen
(als Punkte aufgefaßt) auf der Ebene. Das Skalarprodukt
aller Ebenenpunkte (als Vektoren geschrieben) mit dem
Normalenvektor ist konstant.