Binary Space Partitioning

Unter Binary Space Partitioning (BSP) versteht man einen Objektraum-Algorithmus, der die Lage der Objekte untereinander berücksichtigt.

Zunächst wird im Vorhinein ein BSP-Tree konstruiert, in dem die räumliche Anordnung der Objekte repräsentiert ist. Dann wird für jedes Frame der Betrachterstandpunkt mit dieser Datenstruktur verglichen, um die Sichtbarkeit der einzelnen Flächen zu ermitteln.

Die binären Knoten des BSP-Trees enthalten jeweils eine $n-1$-dimensionale Hyper-Ebene, die den $n$ dimensionalen konvexen Gesamtraum ($C_i$ in Abb. 16.2.2b) in zwei konvexe Halbräume ($C_{i+1}$ und $C_{i+2}$) unterteilt. Zusätzlich enthalten sie zwei Verweise auf Unterbäume, die jeweils einen der beiden Halbräume repräsentieren. Diese rekursive Unterteilung führt im dreidimensionalen Fall dazu, daß der gesamte $\mathbb{R}^3$ durch die Knotenebenen in viele (kleine) konvexe Teilräume zerlegt wird (s. Abb 16.6).

Die Ebenen im Baum sind identisch mit den Flächen der Objekte, d.h. der aktuelle Teilraum des Vaterknotens wird bzgl. dieser Polygonfläche in einen Bereich zerlegt, der ''vor'' der Fläche liegt und in einen Bereich, der ''hinter'' der Fläche liegt. Alle Punkte im Raum vor der Fläche sind von ihr aus sichtbar (bzw. die Fläche ist von jedem Punkt dieses Raumes aus sichtbar) und alle Punkte im Raum hinter der Fläche sind von der Fläche aus unsichtbar (bzw. die Fläche ist von jedem Punkt des Raumes aus unsichtbar).

Abbildung 16.6: Gesamte Szene als BSP-Tree; zuletzt wurde Seite 3 des Dreiecks in den Baum aufgenommen. Dabei sind C13 und C14 aus C12 entstanden.

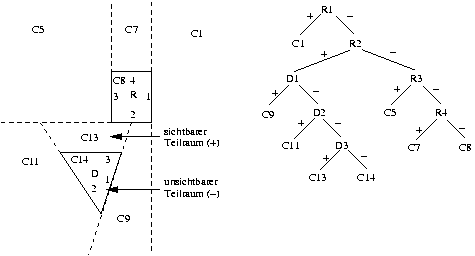
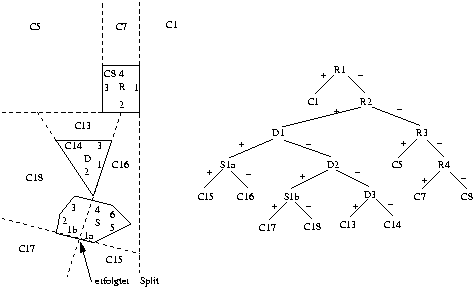
Alle Flächen aller Körper der Szene werden in den BSP-Tree eingefügt (s. Abb 16.6). Dabei kommt es vor, daß eine neu einzufügende Fläche eine (oder mehrere) der Knotenebenen schneidet. Die Fläche wird dann an der Knotenebene in zwei Teilflächen zerschnitten, die jeweils komplett in einem der beiden Teilräume liegen (s. Abb. 16.7). Da im average case $O(n\cdot \log n)$ und im worst case $O(n^2)$ Polygone durch Splits enstehen, ist die Konstruktion des BSP-Trees zu aufwändig, um in Echtzeit zu geschehen. Sie wird offline durchgeführt und daher eignet sich der BSP-Tree nur für statische Szenen.

Abbildung 16.7: Neue Szene: Das Sechseck S kommt hinzu. Kante 1 des Sechsecks wurde beim Aufnehmen geteilt. Kante 3 wird auch geteilt werden, wenn sie aufgenommen wird.

Jedes Blatt des Baums repräsentiert eine (Teil-)Fläche der Szene.

Pro Frame wird der BSP-Tree bzgl. des aktuellen Betrachterstandpunkts traversiert, um die Tiefensortierung zu erreichen. In jedem inneren Knoten gilt:

Die Flächen im Teilraum, in dem sich auch der Betrachter befindet, sind näher am Betrachter als die Flächen, die sich jenseits der Ebene (also im anderen Teilraum) befinden.

Ziel ist es, eine lineare Liste der Flächen aufzubauen, in der sich die am weitesten vom Betrachter entfernte Fläche am Listenanfang befindet und die am wenigsten entfernte am Listenende (back to front order). Deswegen wird in jedem Knoten zunächst in den Teilraum abgestiegen, in dem sich der Betrachter nicht befindet. Erst, wenn alle Flächen aus diesem Raum in die Liste eingefügt wurden, wird der Teilraum, in dem sich der Betrachter befindet, rekursiv untersucht.

Im einfachsten Fall werden anschließend die Polygone gemäß der Liste auf den Bildschirm gezeichnet. Dabei muß beim Setzen eines Pixels kein Test bzgl. der $z$-Werte mehr durchgeführt werden. Allerdings werden weiterhin viele Pixel mehrfach gesetzt, da die Polygone sich zum Teil überdecken.

Dieser Nachteil kann beseitigt werden, wenn die Liste von hinten abgearbeitet wird. Dann wird das vorderste Polygon zuerst gezeichnet. Beim Zeichnen der weiteren Polygone muß darauf geachtet werden, daß deren verdeckte Teile nicht gezeichnet werden. Dies kann z.B. erreicht werden, indem man beim Zeichnen einen 2D-BSP-Tree aufbaut, indem man alle Polygone anhand der bereits gezeichneten in komplett sichtbare und komplett unsichtbare Teile zerlegt.