Span-Buffer

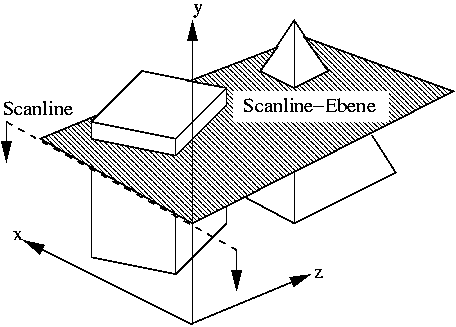
Der z-Buffer-Algorithmus muß für jedes Pixel einer Scanline die z-Koordinate berechnen, um zu entscheiden, ob dieses Pixel gesetzt wird oder nicht. Selbst wenn es gesetzt wurde, kann es sein, daß das Pixel später von einem Polygon, das noch näher am Betrachter liegt, überschrieben wird.

Der Span-Buffer-Algorithmus löst diese beiden Probleme. Normalerweise wird ein Polygon für mehrere aufeinanderfolgende Pixel einer Scanline vorherrschend sein. Ein solcher Scanline-Abschnitt, wird Span genannt. Der Algorithmus ermittelt für jede Scanline, welches Polygon in welchem Span vorherrschend ist. Dadurch können die z-Werte der Punkte innerhalb des Spans interpoliert werden und müssen nicht einzeln berechnet werden. Außerdem wird jeder Span genau einmal gezeichnet, es muß also kein Pixel mehrfach eingefärbt werden. Dieser Effizienzsteigerung steht zusätzlicher Aufwand zur Ermittlung der Spans entgegen.

Pro Scanline wird der Span-Buffer einmal aufgebaut.

a) Scanline-Ebene schiebt sich durch die Szene

b) Schnittfiguren innerhalb einer Scanline-Ebene

Der Abtastzeilenalgorithmus schiebt eine Ebene, die parallel zur $x z$-Ebene ist, die $y$-Achse herunter (s. Abb. 16.2.2a). Diese Ebene schneidet ggf. einige Objekte. Die Schnitte mit den Flächen der Objekte sind Punkte oder Strecken (Span). Damit ist das Problem auf zwei Dimensionen ($x$ und $z$) reduziert (s. Abb. 16.2.2b).

Die Schnittfiguren bestimmen die Spans.

a) Nur die Spans der Vorderseiten werden betrachtet.

b) Teilung der Spans bzgl. der Endpunkte von anderen Spans.

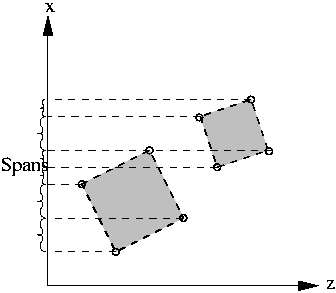
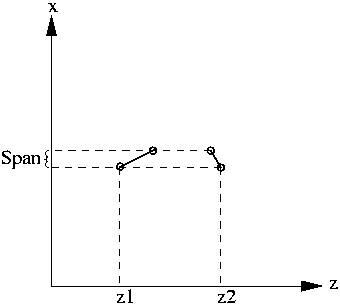
Dann werden die Spans der Vorderflächen nach ihren $x$-Werten sortiert (s. Abb. 16.2.2a) und anschließend miteinander verglichen. Jeder Span wird an allen - innerhalb seines Intervalls liegenden - $x$-Werten der anderen Spans in zwei neue Spans zerschnitten (s. Abb. 16.2.2b).

Ermittlung des vorherrschenden Polygons.

a) Zwei Polygone im selben Span. Das linke Polygon ist vorherrschend.

b) Probleme bei sich durchdringenden Seiten.

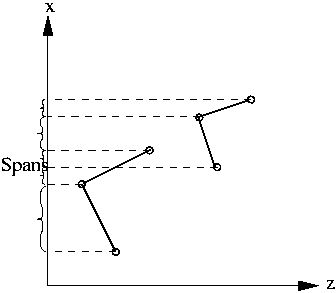
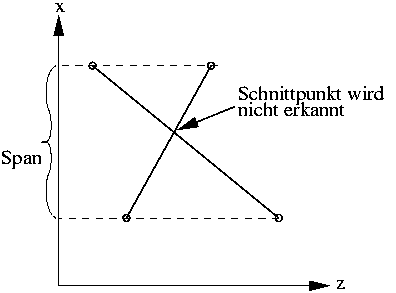
Hierbei ist zu beachten, daß einander durchdringende Polygone (und damit sich schneidende Spans) nicht an ihrem Schnittpunkt in je zwei neue Spans zerlegt werden. Der Algorithmus versagt in diesem Fall und erzeugt keine korrekte Darstellung (s. Abb. 16.2.2b). Jetzt ist eine Liste von Gruppen mit deckungsgleichen Spans enstanden. Für jede Gruppe muß nur entschieden werden, welcher Span dem Betrachter am nächsten liegt. 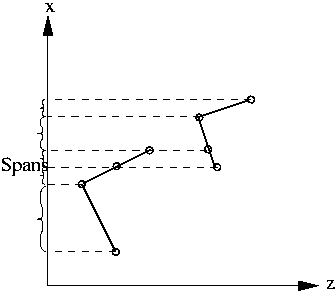Dazu werden für die Anfangspunkte der Spans die $z$-Werte berechnet. Die $z$-Werte der Endpunkte müssen nicht berechnet werden, da ein Span, der am Anfangspunkt vorherrschend ist, auch am Endpunkt vorherrscht (weil keine Spans existieren, die sich schneiden) (s. Abb. 16.2.2a).
Die entstandene Liste von Spans wird anschließend noch danach untersucht, ob benachbarte Spans ursprünglich vom selben Polygon stammen. Wenn ja, werden sie wieder zu einem Span zusammengefaßt und erst dann auf dem Bildschirm dargestellt.

Der Aufwand zur Ermittlung der Spans ist allerdings so hoch, daß der Vorteil gegenüber dem z-Buffer mit steigender Polygonanzahl schwindet.

Falls die Polygone in korrekter $z$-Sortierung vorliegen, kann man mit Hilfe von einem SpanBuffer-Baum oder einem C-Buffer eine weitere Effizienzsteigerung erreichen.

Einfache Szene aus einem Rechteck (R) und einem Dreieck (D). Erste Schritte beim Aufbau eines 2D-BSP-Trees. Die Knotenhyperebenen sind im 2D-Fall Geraden.

a) Szene und BSP-Tree nachdem, die Seite 1 des Rechtecks R als Wurzelebene aufgenommen wurde.

b) BSP-Tree nach Einordnen der Seite 2 des Rechtecks R.