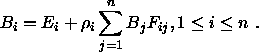
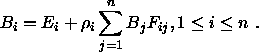
mit
| von der Fläche |
||
| Reflexionsvermögen der Fläche |
||
| Anzahl der Flächen | ||
| Anteil an der von Fläche |
||
| gesamte von Fläche |
Die Gleichung besagt, daß die Energie, die eine Flächeneinheit
verläßt, aus der Summe des abgestrahlten und des reflektierten Lichts
besteht.
Das reflektierte Licht berechnet sich aus der Summe des einfallenden
Lichts, multipliziert mit dem Reflexionsvermögen.
Das einfallende Licht besteht wiederum aus der Summe des Lichts,
das alle Flächen der Szene verläßt, multipliziert mit dem
Lichtanteil, der eine Flächeneinheit des empfangenden Flächenelements
erreicht.
![]() ist der Betrag des Lichts, das die ganze
Fläche
ist der Betrag des Lichts, das die ganze
Fläche ![]() verläßt und eine Flächeneinheit von Fläche
verläßt und eine Flächeneinheit von Fläche ![]() erreicht.
erreicht.
Zwischen den Formfaktoren in diffusen Szenen besteht eine
nützliche Beziehung:
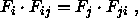
wobei ![]() und
und ![]() die Flächeninhalte sind.
die Flächeninhalte sind.
Umordnen der Ausdrücke liefert
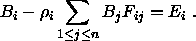
Also kann der Austausch von Licht innerhalb der Flächenelemente
der Szene durch ein Gleichungssystem ausgedrückt werden:
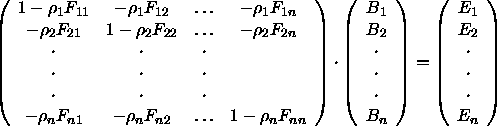
Man beachte, daß der Beitrag eines Flächenelements zu seiner eigenen reflektierten Energie berücksichtigt werden muß (es könnte zum Beispiel konkav sein). Daher haben im allgemeinen nicht alle Terme auf der Diagonalen den Wert Eins.
Wenn man die Gleichung löst, erhält man für jedes Flächenelement einen Strahlungswert. Die Elemente können dann für jeden gewünschten Blickpunkt mit einem gewöhnlichen Algorithmus zur Ermittlung sichtbarer Flächen gerastert werden. Die Strahlungswerte sind die Intensitäten dieses Elements.
Gauß-Seidel-Iterations-Verfahren zur Lösung von linearen Gleichungssystemen
Die ![]() -te Gleichung eines linearen Gleichungssystems
-te Gleichung eines linearen Gleichungssystems
![]() lautet:
lautet:
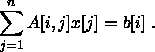
Wenn alle Diagonalelemente von ![]() ungleich Null sind, gilt:
ungleich Null sind, gilt:

Das Iterations-Verfahren startet mit einer Schätzung
![]() , die auf der rechten Seite eingesetzt wird zur
Berechnung von
, die auf der rechten Seite eingesetzt wird zur
Berechnung von ![]() .
Im nächsten Schritt wird zur Berechnung von
.
Im nächsten Schritt wird zur Berechnung von
![]() bereits
bereits ![]() benutzt.
Ein Iterationsschritt lautet also:
benutzt.
Ein Iterationsschritt lautet also:
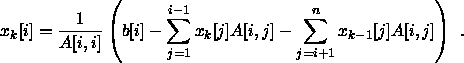
Bei Konvergenz wird das Verfahren nach ![]() Iterationsschritten abgebrochen,
wenn
Iterationsschritten abgebrochen,
wenn ![]() genügend klein geworden ist.
genügend klein geworden ist.