Rotation

Drehung des Objekts bzgl. eines Fixpunktes um einen Winkel $\beta$. Der Fixpunkt liege im Ursprung.

Abbildung 6.4: Rotation um den Winkel $\beta$ bzgl. des Ursprungs

$$\begin{eqnarray*} \sin(\alpha + \beta)&=& \cos (\beta ) \cdot \sin (\alpha ) + \... ...tarrow x' & = & x \cdot \cos (\beta ) - y \cdot \sin (\beta )\\ \end{eqnarray*}$$

Positive Werte für den Drehwinkel $\beta$ bewirken eine Rotation gegen den Uhrzeigersinn.
Vorsicht: Auf dem Bildschirm ist es andersherum, da die $y$-Achse nach unten zeigt.
Bei Wahl eines beliebigen Rotationszentrums $(R_{x}, R_{y})$ folgt für den Punkt $P$

1. Translation um $(-R_{x}, -R_{y})$ liefert $P_1$
2. Rotation bzgl. Ursprung um Winkel $\beta$ liefert $P_2$
3. Translation um $(R_{x}, R_{y})$ liefert $P_{3} = P'$

Abbildung 6.5: Rotation des Punktes $P$ um 90 Grad bzgl Punkt $R$

/****************************************************************************************/
/*                                                                                      */
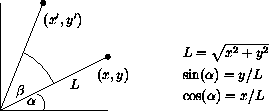
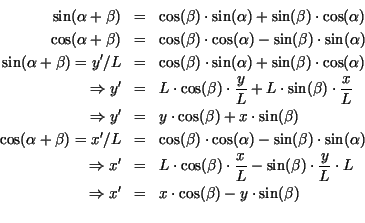
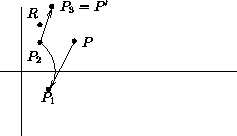
/*                      Skalieren und Rotieren eines Polygons                           */
/*                      Obacht: Da die Polygon-Koordinaten ganzzahlig sind,             */
/*                      verstaerken sich die Rundungsfehler nach jeder Transformation   */
/*                                                                                      */
/****************************************************************************************/

private static final double DEG_TO_RAD = Math.PI/180.0; // Umrechnung Grad in Bogenmass

private void skalier_polygon(           // skaliert ein Polygon
                        Point[] points, // gespeichert im Array points
                        int n,          // mit n Eckpunkten
                        double sx,      // in x-Richtung um den Faktor sx
                        double sy,      // in y-Richtung um den Faktor sy
                        Point  z)       // bezueglich des Punktes z
{
        int i;
        for (i=0; i< n; i++) {
 
                points[i].x = (int)((points[i].x - z.x ) * sx + z.x + 0.5);
                points[i].y = (int)((points[i].y - z.y ) * sy + z.y + 0.5);
 
        }
}

 
private void rotate_polygon(            // rotiert ein Polygon
                        Point[] points, // gespeichert im Array points
                        int   n,        // mit n Eckpunkten
                        int   g,        // um einen Winkel von g Grad
                        Point z)        // bezueglich des Punktes z
{
        int i;
      double beta = g * DEG_TO_RAD;   // Winkel im Bogenmass
        Point P = new Point();
 
        for (i=0; i < n; i++) {
 
                P.x = (int)((points[i].x - z.x ) * Math.cos( beta ) -
                      (points[i].y - z.y ) * Math.sin( beta ) + z.x + 0.5);
 
                P.y = (int)((points[i].y - z.y ) * Math.cos( beta ) +
                      (points[i].x - z.x ) * Math.sin( beta ) + z.y + 0.5);
 
                points[i].x = P.x;
                points[i].y = P.y;
 
        }
}