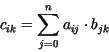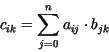Häufig werden mehrere Transformationen hintereinander auf ein Objekt
angewendet.
Es entstehen Rundungsfehler, wenn nach jeder Einzel-Transformation
die ganzzahligen Koordinaten bestimmt werden.
Deshalb sollten mehrere Transformationen zu einer zusammengesetzt werden.
Dies ist mit Hilfe von Matrizen, die die Transformationen repräsentieren,
möglich. Durch Matrizenmultiplikation (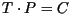 ) der
Transformationsmatrix
) der
Transformationsmatrix 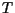 und dem als einspaltige Matrix interpretierten
Koordinatenvektor
und dem als einspaltige Matrix interpretierten
Koordinatenvektor 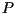 wird die eigentliche Transformation
durchgeführt. Die einzelnen Elemente
wird die eigentliche Transformation
durchgeführt. Die einzelnen Elemente 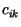 der Ergebnismatrix
der Ergebnismatrix 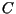 errechnen sich aus den Elementen der Eingangsmatrizen
errechnen sich aus den Elementen der Eingangsmatrizen 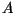 und
und 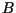 wie
folgt:
wie
folgt:
Eine Skalierung sieht dann z.B. folgendermaßen aus:
Eine Rotation hat folgendes Aussehen:
Die Reihenfolge von Matrix und Vektor kann vertauscht werden. Allerdings
müssen dann beide transponiert werden: