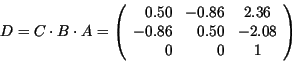Homogene Koordinaten

Um auch die Translation durch eine Matrixmultiplikation ausdrücken zu können, muß das Konzept der homogenen Koordinaten eingeführt werden. Dabei wird unserem Objektraum eine Dimension hinzugefügt, es werden aber weiterhin 2D-Objekte repräsentiert und dargestellt.

Ein Punkt $P=(x,y)$ hat die homogenen Koordinaten $(x_{h} \; y_{h} \; w)^T$ mit $w \neq 0$ und

$$\begin{eqnarray*} x_h&=&x \cdot w\\ y_h&=&y \cdot w \end{eqnarray*}$$

Beispiel:

Das homogene Koordinatentripel $(6 \; 8 \; 2)^T$ gehört zum Punkt $P =(3, 4)$. Derselbe Punkt hat die homogenen Koordinaten $(3 \; 4 \; 1)^T$. D.h. jeder Punkt $P=(x,y)$ repräsentiert eine ganze Ursprungsgerade im 3D-Raum.

Der Richtungsvektor $\vec{r}$, der vom Ursprung zum Punkt $R = (x, y)$ führt, hat die homogenen Koordinaten $(x\; y \;0)^T$.

Abbildung 6.6: Punkt $(3,4)$ und Richtungsvektor $(3 ; 4)^T$

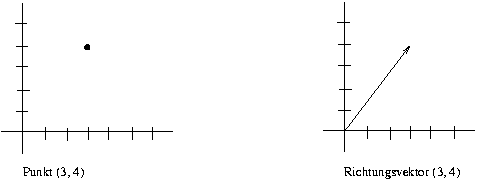
Die Transformationen Translation, Skalierung und Rotation werden nun als $3 \times 3$-Matrizen realisiert. Zusammengesetzte Transformationen ergeben sich durch Matrix-Multiplikation.

Translation

$$\left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right) :=... ...left( \begin{array}{c} x+t_x \\ y+t_y \\ 1 \end{array} \right)$$

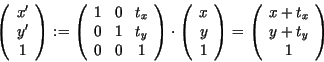
Skalierung

$$\left ( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right ) ... ...array}{c} x \cdot s_x \\ y \cdot s_y \\ 1 \end{array} \right )$$

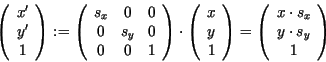
Rotation

$$\left ( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right ) ... ...n (\beta ) + y \cdot \cos (\beta ) \\ 1 \end{array} \right )$$

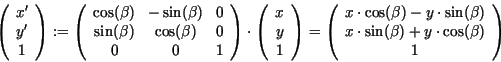
Für die Auswertung einer zusammengesetzten Transformation

• gilt das Assoziativgesetz, d.h. $A \cdot B \cdot C = (A \cdot B)\cdot C = A \cdot (B \cdot C)$,
• gilt im allgemeinen nicht das Kommutativgesetz, d.h. $A \cdot B \neq B \cdot A$.
  

Beispiel:

Translation um $(-3, -1)$ mit anschließender Rotation um $90^{\circ}$ ist verschieden von Rotation um $90^{\circ}$ mit anschließender Translation um $(-3, -1)$.

Beispiel:

Rotation bzgl. $(3, 1)$ um $60^{\circ}$

Matrix für Translation um $(-3, -1)$ lautet

$$A= \left( \begin{array}{rrc} 1 & 0 & -3\\ 0 & 1 & 1\\ 0 & 0 & 1 \end{array}\right)$$

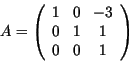
Matrix für Rotation um $60^{\circ}$ lautet

$$B = \left( \begin{array}{rcc} 0.50 & -0.86 & 0.00\\ 0.86 & 0.50 & 0.00\\ 0.00 & 0.00 & 1.00 \end{array}\right)$$

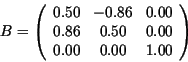
Matrix für Translation um $(3, 1)$ lautet

$$C = \left( \begin{array}{ccc} 1&0 & 3\\ 0&1 & 1\\ 0&0 & 1 \end{array}\right)$$

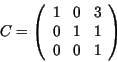
Matrix für gesamte Transformation lautet

$$D = C \cdot B \cdot A = \left( \begin{array}{rrc} 0.50 & -0... ...2.36\\ -0.86 & 0.50 & -2.08 \\ 0 & 0 & 1 \end{array}\right)$$