Affine Abbildungen und Invarianz

Affine Abbildungen bestehen aus einer linearen Abbildung und einem translativen Anteil:

$$B\vec{x} = A\vec{x} + \vec{t}$$

Es handelt sich um eineindeutig umkehrbare Abbildungen, bei denen

• Geradlinigkeit,

• Zusammengehörigkeit (Objekt wird nicht zerissen),

• Parallelität und

• Teilverhältnisse auf jeder Geraden

erhalten bleiben. Wogegen

• Positionen,
• Längen,
• Winkel,
• Flächeninhalte und

• Orientierungen (Umlaufsinn)

sich ändern können.

Alle bisher in der Vorlseung behandelten Transformationen sind lineare Abbildungen.

Invarianz unter linearen Abbildungen bedeutet in diesem Zusammenhang, daß es keinen Unterschied macht, ob erst die Kurve gezeichnet und dann jeder der gezeichneten Kurvenpunkte abgebildet wird oder ob die Stützpunkte abgebildet werden und die Kurve dann auf Basis diesen neuen Stützpunkte gezeichnet wird.

$$\begin{eqnarray*} B\vec{x} = B (\sum_{ i=0}^n m_i \vec{p_i} ) &=& A ( \sum_{i=0... ...m_i ( A \vec{p_i} + \vec{t}) \\ &=& \sum_{i=0}^n m_i B\vec{p_i} \end{eqnarray*}$$

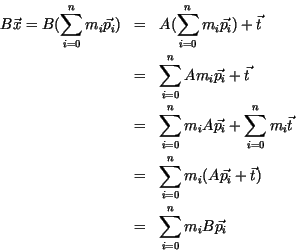
Natürlich ist die zweite Variante viel weniger rechenaufwändig. Darüberhinaus kann es (z.B. bei einer uniformen Skalierung mit dem Faktor 2) vorkommen, daß die transformierten Kurvenpunkte auf dem Bildschirm nicht mehr benachbart sind. Ein Effekt, der vermieden wird, wenn erst die Stützpunkte transformiert und dann die Kurvenpunkte berechnet werden.