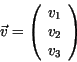
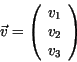
Gegeben seien zwei 3D-Vektoren
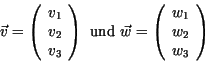
Das Kreuzprodukt
von ![]() und
und ![]() ist definiert als
ist definiert als
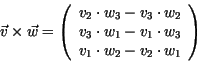
Der Vektor
![]() steht senkrecht auf
steht senkrecht auf ![]() und steht senkrecht
auf
und steht senkrecht
auf ![]() .
Seine Länge entspricht der Fläche des durch
.
Seine Länge entspricht der Fläche des durch ![]() und
und ![]() aufgespannten Parallelogramms, d.h.
aufgespannten Parallelogramms, d.h.
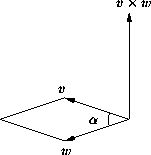
In einem rechtshändigen Koordinatensystem entspricht bei
gespreizten Fingern der Daumen ![]() , der Zeigefinger
, der Zeigefinger ![]() , der
Mittelfinger
, der
Mittelfinger
![]() .
.