Transformation der Normalenvektoren

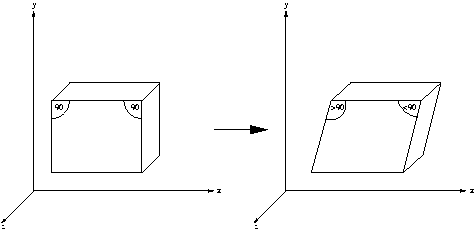
Die Normalenvektoren müssen bei der Transformation von Objektpunkten ebenfalls abgebildet werden. Wenn diese Transformation z.B. eine nicht-uniforme Skalierung ist, dann bleiben die Winkel zwischen einzelnen Flächen nicht erhalten.

Winkeluntreue unter nicht uniformer Skalierung

Wenn die Normale $\vec{n}$ mit derselben Matrix $M$ transformiert wird, wie die Objektpunkte einer Fläche $F$, ist $\vec{n}$ anschließend evtl. nicht mehr senkrecht zu $F$.

Wie muß $\vec{n}$ transformiert werden?

Gegeben seien zwei Punkte $P_1 = (p_{1x}, p_{1y}, p_{1z}, 1)$ und $P_2 = (p_{2x}, p_{2y}, p_{2z}, 1)$, die in der Fläche $F$ liegen und die Normale $\vec{n} = (n_x \; n_y \; n_z \; 0)^T$. Weiterhin sei die Transformationsmatrix $M$ gegeben. Es gilt:

$$P_1' = M P_1 \;\; \mbox{und} \;\; P_2' = M P_2$$

wobei die Punktkoordinaten als Spaltenvektoren aufzufassen sind.

Der Vektor

$$\vec{r} = P_2 - P_1$$

liegt in der Ebene von $F$ und ist deshalb senkrecht zu $\vec{n}$:

$$\vec{r} \cdot \vec{n} = 0$$

Diese Beziehung soll auch für die projizierten Vektoren $\vec{n}'$ und

$$\vec{r}' = P_2' - P_1' = M P_2 - M P_1 = M (P_2 - P_1) = M \vec{r}$$

gelten:

$$\vec{n}' \cdot \vec{r}' = 0$$

Vorletzte Gleichung ausnutzen ergibt

$$\vec{n}' \cdot M \vec{r} = 0$$

Matrizenmultiplikation ausführen und Skalarprodukt ausführlich schreiben (dabei $n_w' = 0$ ausnutzen):

$$\begin{eqnarray*} n_x'(m_{11}r_x + m_{12}r_y + m_{13}r_z + m_{14}) & + & \\ n_y... ... & \\ n_z'(m_{31}r_x + m_{32}r_y + m_{33}r_z + m_{34}) & = & 0 \end{eqnarray*}$$

Nach den Komponenten von $\vec{r}$ sortieren:

$$\begin{eqnarray*} r_x(m_{11}n_x' + m_{21}n_y' + m_{31}n_z') & + & \\ r_y(m_{12}... ..._z') & + & \\ 1 (m_{14}n_x' + m_{24}n_y' + m_{34}n_z') & = & 0 \end{eqnarray*}$$

Matrixmultiplikation und Skalarprodukt erkennen und kompakt schreiben:

$$\vec{r} \cdot \left( \begin{array}{ccc} m_{11} m_{21} m_{31... ...m_{44} \end{array}\right) \vec{n}' = \vec{r} \cdot \vec{n} = 0$$

Die Matrix ist die Transponierte $M^T$ zu $M$.

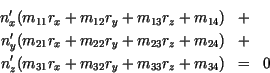
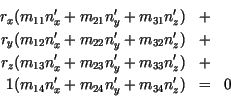
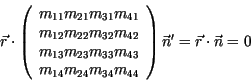
Es gilt also

$$\vec{n} = M^T \vec{n}'$$

Nach $\vec{n}'$ auflösen, indem zunächst alles transponiert wird

$$\vec{n}^T = \vec{n}'^T M$$

Dann mit $M^{-1}$ von rechts multiplizieren

$$\vec{n}^T M^{-1} = \vec{n}'^T$$

Alles nochmal transponieren und die Seiten der Gleichung tauschen

$$\vec{n}' = (M^{-1})^T \vec{n}$$

Es gilt also, daß bei der Transformation eines Objekts mit der Matrix $M$ ein Normalenvektor $\vec{n}$ dieses Objekts mit der transponierten Inversen von $M$ abgebildet werden muß.