Normalprojektionen

Stehen die Sehstrahlen normal zur Bildebene, liegt eine orthogonale Projektion vor.

Abbildung 12.4: Grund-, Seiten-, Aufriss (a) bzw. axononometrische Projektion (b)

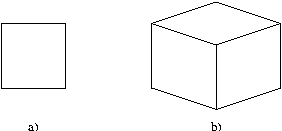
Die häufigste Anwendung orthogonaler Projektionen liegt in der Darstellung eines Objekts durch Grund-, Auf- und Seitenriß (Abbildung 12.4 a).

Eine weitere Form der Normalprojektionen sind die axonometrischen Projektionen, bei denen die Bildebene auf keiner der Körper-Hauptachsen senkrecht steht. Dadurch sind in der Abbildung mehrere zueinander normal stehende Flächen gleichzeitig sichtbar. Die resultierenden Darstellungen sind der perspektivischen Projektion ähnlich. Anstelle der zur Entfernung vom Auge proportionalen Verkürzung erfolgt aber eine gleichmäßige Verkürzung aller Kanten (Abbildung 12.4 b).

Die Transformationsmatrix für die orthogonale Parallelprojektion auf die $x y$-Ebene lautet

$$P_{{ortho}_{xy}} = \left [ \begin{array}{cccc} 1 & 0 & 0 & 0... ... & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ \end{array} \right],$$

da für jeden Punkt $P = (x, y, z, 1)$ die Koordinaten des projizierten Punktes gleich $(x, y, 0, 1)$ sind.