Bei den schiefen Parallelprojektionen stehen die Sehstrahlen
nicht normal auf der Bildebene,
sondern schneiden sie unter dem Winkel ![]() (Abbildung
12.5
).
Die schiefe Projektion auf die
(Abbildung
12.5
).
Die schiefe Projektion auf die ![]() -Ebene
entspricht einer Scherung der
-Ebene
entspricht einer Scherung der ![]() - und
- und ![]() -Koordinaten proportional
zu
-Koordinaten proportional
zu ![]() .
.
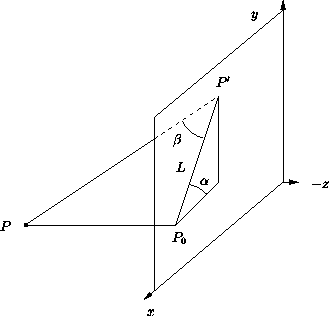
Seien
![]() die orthogonale und
die orthogonale und
![]() die schiefe Projektion von Punkt
die schiefe Projektion von Punkt ![]() .
Sei
.
Sei ![]() die Entfernung von
die Entfernung von ![]() nach
nach ![]() .
Dann gilt
.
Dann gilt
Wegen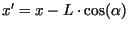
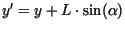
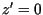
Der Winkel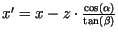
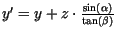
Die Koordinaten zweier projizierter Punkte
![]() ,
, ![]() lauten:
lauten:
Für zwei Punkte, die sich nur bzgl. ihrer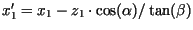
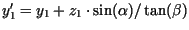
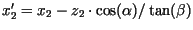
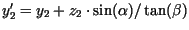
für den Abstand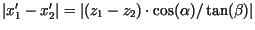
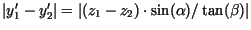
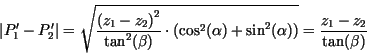
Für die Berechnung der Transformationsmatrix benötigt der Algorithmus
den Verkürzungsfaktor ![]() und den Scherwinkel
und den Scherwinkel ![]() .
.
![]() gibt an,
um welchen Faktor zur Bildebene normal stehende Strecken verkürzt werden.
Es gilt
gibt an,
um welchen Faktor zur Bildebene normal stehende Strecken verkürzt werden.
Es gilt
![]() definiert den Winkel zur Horizontalen, unter dem diese Kanten
aufgetragen werden.
Für die Koordinaten des so projizierten Punktes
definiert den Winkel zur Horizontalen, unter dem diese Kanten
aufgetragen werden.
Für die Koordinaten des so projizierten Punktes
![]() gilt
gilt
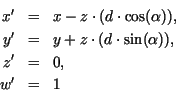
Die entsprechende Transformationsmatrix lautet
![\begin{displaymath}
P_{{schief}_{xy}}(\alpha, d) = \left [ \begin{array}{cccc}
1...
...pha ) & 0\\
0& 0& 0 & 0\\
0 & 0 & 0 & 1
\end{array} \right].
\end{displaymath}](img599.gif)
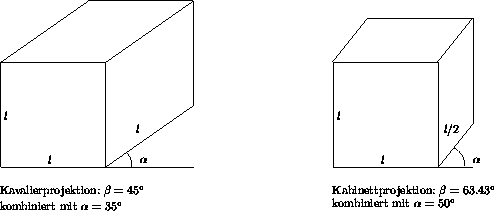
Zwei häufig als Ersatz für Perspektive verwendete Projektionen haben die
Werte ![]() (
(
![]() ),
),
![]() (Kavalierprojektion) und
(Kavalierprojektion) und
![]() (
(
![]() ),
),
![]() (Kabinettprojektion).
Bei der
Kavalierprojektion werden alle auf der Bildebene normal stehenden
Strecken unverkürzt abgebildet.
Bei der Kabinettprojektion
ergibt sich eine Verkürzung auf die Hälfte ihrer ursprünglichen Länge.
(Kabinettprojektion).
Bei der
Kavalierprojektion werden alle auf der Bildebene normal stehenden
Strecken unverkürzt abgebildet.
Bei der Kabinettprojektion
ergibt sich eine Verkürzung auf die Hälfte ihrer ursprünglichen Länge.