Kugel

Die Oberfläche einer Kugel mit Radius 1 kann beschrieben werden durch

$$( \sin (\theta ) \cos ( \phi ), \sin (\theta ) \sin (\phi ), \cos (\theta )), 0 \leq \phi < 2 \pi , 0 \leq \theta < \pi\ .$$

Zur Approximation durch Flächen wird der Vollwinkel in $n$ Teile zerlegt:

$$\alpha = ( 2 \pi ) / n,\ \ n \in \mathbb{N}\mbox{ gerade }.$$

Dadurch entstehen auf der Kugel $n / 2$ gleichgroße Längenkreise und $(n / 2 - 1)$ verschieden große Breitenkreise. Diese schneiden $n$ Dreiecke an jedem Pol und $n(n / 2 - 2)$ Vierecke aus der Kugeloberfläche. Die Ortsvektoren der Eckpunkte eines Dreiecks am Nordpol $( \theta = 0 )$ lauten

$$(0, 0, +1, 1),\\ (\sin (\alpha ) \cos ( \phi ), \sin (\alph... ... \sin (\alpha ) \sin ( \phi + \alpha ), \cos (\alpha ), 1),\\$$

mit $\phi = k \cdot \alpha$, $k \in \{0,..., n-1\}$.

Die Eckpunkte eines der Vierecke haben die Ortsvektoren

$$(\sin (\theta ) \cos (\phi ), \sin (\theta ) \sin (\phi ), \... ... \theta + \alpha ) \sin (\phi ), \cos ( \theta + \alpha ), 1),$$

mit $\phi = k \cdot \alpha , k \in \mathbb{N}, k < n$ und $\theta = l \cdot \alpha , l \in \mathbb{N}, 0 < l < (n / 2 - 1)$.

Als Normalenvektor wird in jedem Eckpunkt der Ortsvektor als Richtungsvektor ($w = 0$) eingetragen, denn der Radiusvektor steht senkrecht auf der Kugeloberfläche. Einen Ellipsoid erzeugt der Rendering-Algorithmus aus der Kugel durch ungleichmäßige Skalierung beim Modeling.

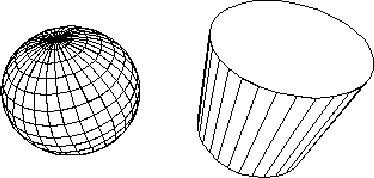
Abbildung 15.3 zeigt eine vom Projektionsalgorithmus erzeugte Szene mit Kugel und Zylinder in der Drahtmodell-Darstellung ohne Rückkanten ($n=32$).

Abbildung 15.3: Kugel und Zylinder als Drahtgitter