Es sollen nun nicht alle Stützpunkte Einfluß auf den gesamten Kurvenverlauf haben und der Grad der Polynome soll unabhängig von der Zahl der Stützpunkte sein.
Spezifiziere die Kurve durch ![]() Stützpunkte
Stützpunkte
![]() und einen Knotenvektor
und einen Knotenvektor
![]() .
.
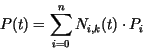
Die Punkte ![]() wirken sich nur auf maximal
wirken sich nur auf maximal ![]() Kurvenabschnitte
aus und werden gewichtet durch die Basis des B-Splines,
Polynome
Kurvenabschnitte
aus und werden gewichtet durch die Basis des B-Splines,
Polynome ![]() vom Grad
vom Grad ![]() (
(
![]() ) :
) :
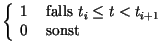 |
(7.1) | ||
| (7.2) |
Bei Division durch Null wird der Quotient gleich ![]() gesetzt.
gesetzt.
Durch die Wahl von ![]() und
und ![]() geht jeder Stützpunkt auf einzigartige
Weise in die Kurve ein.
geht jeder Stützpunkt auf einzigartige
Weise in die Kurve ein. ![]() kann entweder uniform (die
kann entweder uniform (die ![]() sind
äquidistant) oder nicht uniform gewählt werden. Jede der beiden
Arten kann offen (Anfang und Ende von
sind
äquidistant) oder nicht uniform gewählt werden. Jede der beiden
Arten kann offen (Anfang und Ende von ![]() bestehen jeweils aus
bestehen jeweils aus
![]() -mal dem kleinsten bzw. größten
-mal dem kleinsten bzw. größten ![]() ) oder periodsich (es
ergeben sich periodische Gewichtungspolynome, die durch einfaches
Verschieben auseinander hervorgehen) sein.
) oder periodsich (es
ergeben sich periodische Gewichtungspolynome, die durch einfaches
Verschieben auseinander hervorgehen) sein.
Der Knotenvektor wird häufig wie folgt gewählt für
![]() :
:
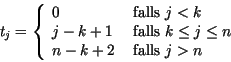
Hierdurch wird ![]() im Intervall
im Intervall ![]() definiert.
definiert.
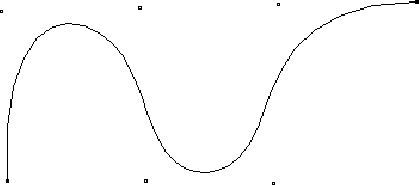
Beispiel: ![]() ,
, ![]() ergibt einen offenen uniformen quadratischen
B-Spline mit dem Knotenvektor
ergibt einen offenen uniformen quadratischen
B-Spline mit dem Knotenvektor
![]() .
Die Stützpunkte
.
Die Stützpunkte
![]() haben nur lokal Einfluß auf den Kurvenverlauf, und zwar in den Intervallen
haben nur lokal Einfluß auf den Kurvenverlauf, und zwar in den Intervallen
![]() .
.
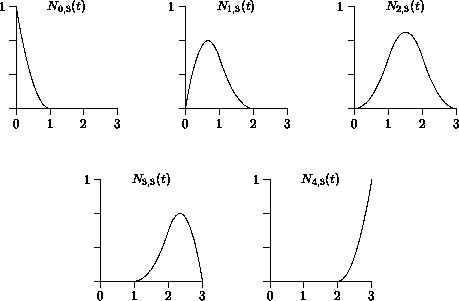
Sonderfall
Für ![]() ergibt sich für den Knotenvektor der Sonderfall
ergibt sich für den Knotenvektor der Sonderfall
Die zugehörigen B-Splinefunktionen haben die schon bekannte Form
Somit lassen sich also die B-Splinefunktionen als Verallgemeinerung der Bernsteinpolynome auffassen.
Wie bei den Bernsteinpolynomen gilt auch für die B-Splinefunktionen
![]() , daß sie positiv sind, und
, daß sie positiv sind, und
![]()